Kinematic redundancy: Kinetics for use with redundant manipulators

Kousuke Okabe, an Associate Professor in the Department of Electrical and Computer Engineering, explores kinematic redundancy and the redundant manipulator using the Grassmann algebra

In recent years, the industrial world has witnessed the launch of manipulators with kinematic redundancy such as those from Yaskawa Electric Corporation’s MOTOMAN-SIA series. However, for many of these, redundancy is applied kinematically, through contact avoidance between the arm and the environment, and not dynamically. The robot’s operations include contact avoidance and turning movements. Much of the time when it is not required, the redundancy is not utilised, but rather consumes more energy due to the increased weight.

The authors are therefore conducting research aimed at improving movement performance and reducing energy consumption by dynamically using the kinematic redundancy of the manipulator. A problem in applying for redundancy dynamically is that the internal movement due to redundancy is generally represented by the projection of subtasks and does not express the internal movement directly.

Since the expression of the internal movement is not generalised, the dynamic characteristics associated with the internal movement are also unclear. The authors have therefore redefined internal movement by generalised redundancy and clarified the dynamic characteristics based on the redefined internal movement and the movement of the hand, which is the workspace.

Formulating internal movement by kinematic redundancy

The internal movement comprises a set of independent joint movements that do not affect hand movement. Therefore, the set of joint velocities (q̇ – space) that realises the hand movement (ṙ ) in the joint velocity space (J⁺ – space) and the orthogonal subspace (U -space) are the set of joint velocities corresponding to the internal movement (ż). A new representation of the generalised internal movement has been defined by finding the basis vectors of this subspace using Grassmann algebra. In the authors’ research, the movement of the arm is a movement in the space comprising the space of hand movement (J⁺ – space) and the space of internal movement due to kinematic redundancy (U -space) and this space is called the extended workspace.

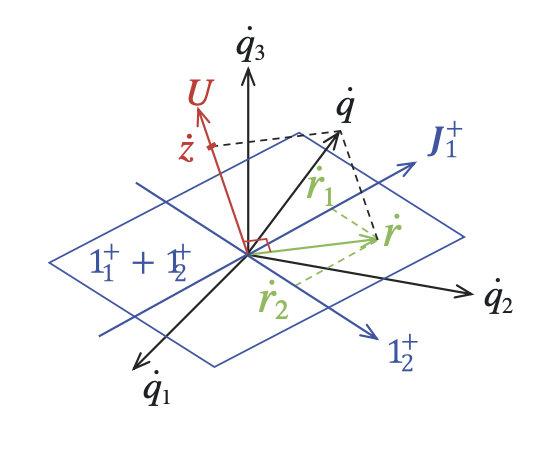
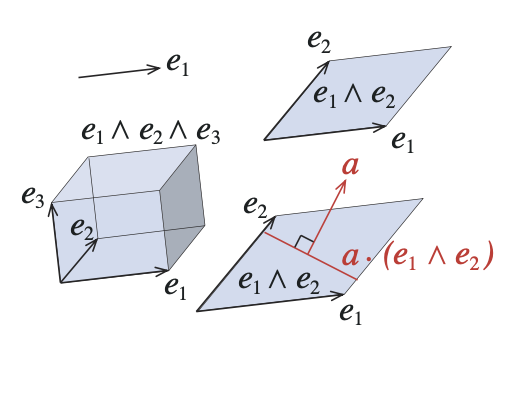
Basis vector derivation using Grassmann algebra (e_i ∧ e_j ) of basis vectors e_i. A single basis vector represents a 1-dimensional space (e₁ ), and the wedge product (e₁∧ e₂) of two basis vectors represents the 2-dimensional plane of the parallelogram with those sides. Therefore, the space representing the hand movement in the joint velocity space is expressed by the wedge product (J⁺₁ ∧ J⁺₂ ) of J⁺₁  representing the movement of the hand in the x-axis direction and J⁺₂  representing the movement in the y-axis direction. The space orthogonal to the hand movement is derived using contraction.

Contraction (e_i • e_j ) has the effect of extracting from the contracted space a subspace that is orthogonal to the contracted space. As a result, the joint velocity space (q̇₁ ∧ q̇₂ ∧ q̇₃ ) is contracted 123 by the space representing the hand movement (J⁺₁ ∧ J⁺₂ ) to obtain the space (U) representing the internal movement due to redundancy.

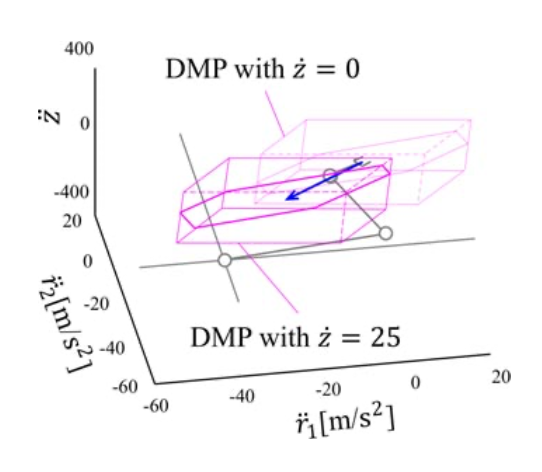
Translation of dynamic manipulability polyhedron/ manipulating force polyhedron

The authors have clarified the dynamic characteristics due to kinematic redundancy by deriving a dynamic manipulability polyhedron that represents the set of hand accelerations that can be output within the joint drive torque limit in the extended workspace. As a result of the analysis, it has been clarified that the dynamic manipulability polyhedron forms a parallel polyhedron in the extended workspace and translates in the extended workspace in proportion to the tensor product of the velocity of the hand movement and the internal movement. Similarly, as a result of analysing the dynamic characteristics of the redundant manipulator for the manipulating force polyhedron representing the set of manipulating forces that can be output within the joint drive torque limit, it has been clarified that the manipulating force polyhedron also constitutes a parallel polyhedron in the extended workspace, and it translates in the extended workspace in proportion to the acceleration of hand movement and internal movement, and in proportion to the tensor product of velocity.

In the future, the aim is to confirm the dynamic characteristics of the redundant manipulator that have been clarified using actual machines and to expect to be able to apply the clarified dynamic characteristics to industrial robots.

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.