The role of neutrinos and Special Relativity in Baryogenesis

It is well known that systems comprising two or more rotating particles or bodies play an important role not only in Astronomy and Chemistry, but also on Nuclear Physics. In Chemistry such systems are known as the Bohr model, whereas in particle physics they are known as the Rotating Lepton Model

The importance of such systems had been already realized by Plato and Aristotle in the Academy of Athens back in the 4th century BC. Thus Aristotle stated that “the cyclic motion is the origin of everything” (Figure 1), emphasizing that this choice leads to stable rotating structures. Consequently, if we choose three identical particles, then the equilateral rotating triangle geometry of Figure 1 is the only reasonable choice. This is the geometry of the Rotating Lepton Model (RLM) of elementary particles ^[1,2]. It could be also called Rotating Neutrino Model (RNM), but as we shall see, electrons and positrons can also participate in the circular motion, thus creating bosons rather than hadrons. Therefore, the acronym RLM is more general and useful. Both the RNM and the RLM satisfy the following two famous statements of the two most cited philosophers of all times, i.e. Plato ^[3] and his student Aristotle ^[4]. Thus, Plato writes in his work “Timeos” that “Everything consists of triangles”, while Aristotle states in his book Mechanica 2 that “The origin of everything is the cycle” (or the “cyclic motion”).

Figure 3 shows the hadron geometry of the RLM for the case of the proton. Its main element is the rotating three-neutrino ring. The center of this ring may be vacant or occupied by a neutrino or antineutrino in the case of neutral hadrons or may be occupied by a positron or electron in the cases of the proton and of the antiproton, respectively. Since the speed of the center of the composite particle relative to a laboratory observer is in general small relative to the speed of light, while the speed of rotation of the rotating leptons with respect to the center of rotation turns out to be very close to the speed of light, it follows that the center of rotation can be viewed as being at rest with respect to the laboratory observer. Therefore the center of rotation can be used as a laboratory reference frame.

In view of the previous discussion, the mathematical formulation of the Rotating Lepton Model (RLM) comprises only three equations.

i. The equation of motion of each of the three neutrinos accounting for Special Relativity (SR) and for the Equivalence Principle (inertial mass equals gravitational mass). According to the preceding discussion, the equation is

ii. The de Broglie equation for each rotating particle

which expresses the dual particle-wave nature of each rotating neutrino by setting its angular momentum equal to the reduced Planck constant ћ.

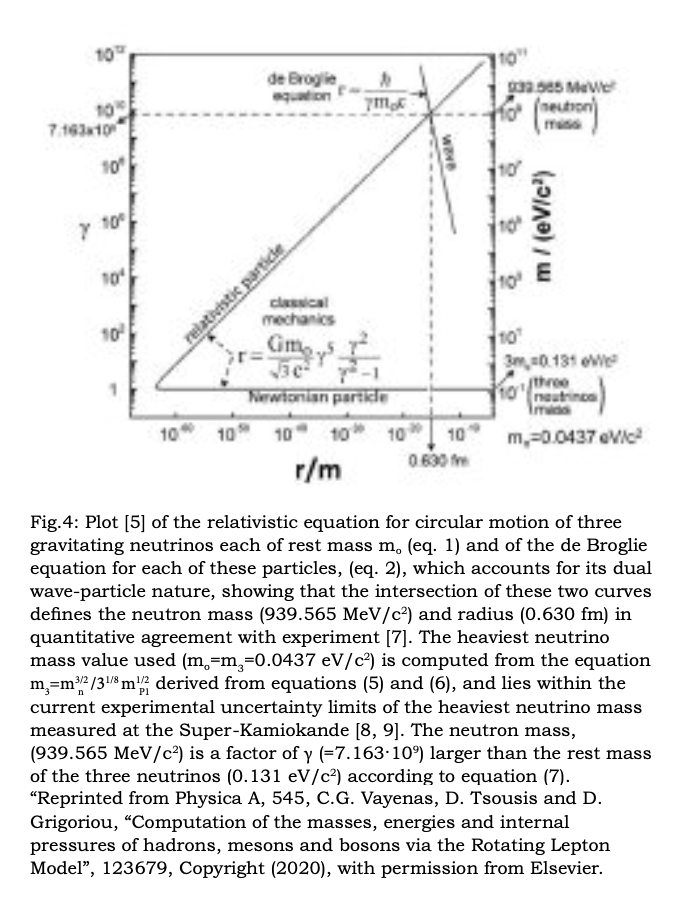
A plot of equations 1 and 2 is shown in Figure 4.

iii. The energy balance equation for the three rotating particles, each of which has, according to the theory of special relativity, an energy computed from

Therefore, the total energy of the three- particle system is

Equations (1), (2), (3) and (4) can be solved analytically as follows:

First we combine equations (1) and (2) to obtain

Then, using v/c≈1 (Fig. 4) it follows that for n=1 (ground state) it is:

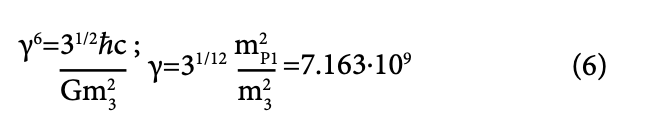
therefore

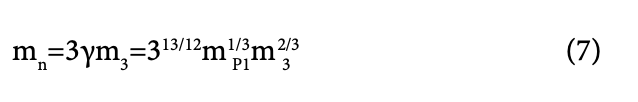
which, considering the heaviest neutrino type, m₃ = 43.7 meV/c² [9], m^Pl= 1.2209.10²⁸ eV/c² =1.2209.10¹⁹ GeV/c² gives m =939.565 MeV/c², which, amazingly, is the neutron mass [10]!

After this remarkable and, at first, unexpected success, one may compute the masses of other hadrons and of bosons. For this, one must choose the model geometry of each composite particle. The procedure is simple and eurestic: Using the experimentally detected decay products of the hadron (or boson) under study, one chooses a composite particle geometry and then applies the RLM methodology to compute the composite particle mass. If it matches the experimental mass value, then it is accepted and adopted. If not, then a new geometry is chosen until a good match (typically ± 2%) to the experimental mass value is obtained. We have found that for the relatively simple, composite particle geometries of Figure 2, two or three tries are usually sufficient to get a good approximation of the mass (± 2%) and thus to obtain a satisfactory model.

The importance of these findings, first reported in a Springer book [1] and several other publications [2, 5-6, 11-14], has been discussed analytically in an article entitled “The Rotating Lepton Model” published in the Research Features Magazine [15].

The RLM combines the de Broglie wavelength equation with the special relativistic equation of motion of the rotating particles, using the equivalence principle of inertial and gravitational mass [16] or, equivalently, using Newton’s universal gravitational law with gravitational, rather than rest, masses, and leads to surprisingly good (typically 1%) agreement with experiment regarding the mass of the composite particles (hadrons and bosons) formed by the rotating leptons (neutrinos or combinations of neutrinos and positrons or electrons). The RLM was initially used to model and to compute the masses of neutrons and protons [5] as well as of bosons [2]. In total, the RLM has been used to derive simple analytical expressions for the rest masses of 9 hadrons, 3 mesons and 3 bosons and to compare the computed values with the corresponding experimental ones [11-14].

REFERENCES

1. “Gravity, special relativity and the strong force: A Bohr-Einstein-de Broglie model for the formation of hadrons”, C.G. Vayenas, S.N.-A. Souentie, Springer, New York, (2012).
2. “Catalysis in Chemistry and Physics: The Roles of Leptons, Special Relativity and Quantum Mechanics”, C.G. Vayenas, D.G. Tsousis, E.H. Martino, Springer Nature, Switzerland AG, (2024). ISBN978-3- 031-68121-9.
3. Timaeus.
4. Mechanica A
5. C.G. Vayenas, D. Tsousis and D. Grigoriou, Computation of the masses, energies and internal pressures of hadrons, mesons and bosons via the Rotating Lepton Model, Physica A, 545 (2020) 123679.
6. C.G. Vayenas, S. Souentie, A. Fokas, “A Bohr-type model of a composite particle using gravity as the attractive force”, Physica A, 405, 360-379 (2014).
7. Burkert, V.D., Elouadrhiri, L. & Girod, F.X. The pressure distribution inside the proton. Nature 557, 396 (2018).
8. R.N. Mohapatra et al (2007) Theory of neutrinos: a white paper. Rep Prog Phys 70:1757-1867.
9. Takaaki Kajita, Discovery of neutrino oscillations. Rep. Prog. Phys. 69, 1607 (2006).
10. D. Griffiths (2008) Introduction to Elementary Particles. 2nd ed. Wiley-VCH. Verlag GmbH & Co. KgaA, Weinheim.
11. C.G. Vayenas, A.S. Fokas, D. Grigoriou, On the structure, mass and thermodynamics of the W± bosons. Physica A, 450 (2016) 37.
12. A.S. Fokas, C.G. Vayenas. On the structure, mass and thermodynamics of the Zo bosons. Physica A, 464, 231-240 (2016).
13. A.S. Fokas, C.G. Vayenas, D. Grigoriou, On the mass and thermodynamics of the Higgs boson. Physica A, 492 (2018) 737.
14. C.G. Vayenas, D. Tsousis, D. Grigoriou, K. Parisis & E. Aifantis, “Hadronization via Gravitational confinement of fast neutrinos: Mechanics at fm distances”, Z. Angew. Math. Mech. 102, e202100158 (2022).
15. “The Rotating Lepton model: Combining fundamental Theories” Research Features 137, 102-105 (2021).
16. Roll PG, Krotkov R, Dicke RG (1964) The equivalence of inertial and passive gravitational mass. Annals of Physics 26(3):442-517.

To read and download this eBook in full ‘The role of neutrinos and Special Relativity in Baryogenesis’ click here