Collective quantum phenomena and their applications

John H. Miller, Jr., University of Houston (UH), from the Dept. of Physics and Texas Center for Superconductivity, explains collective quantum phenomena and their applications

The evidence supporting the quantum behavior of electrons, as well as every other known particle in the universe, is overwhelming. On the centennial anniversary of Max Planck’s seminal paper on energy quantization ⁽¹⁾, Kleppner and Jackiw pointed out, “Quantum theory is the most precisely tested and most successful theory in the history of science”. ⁽²⁾

Collective quantum phenomena explored

Here, we discuss systems that show collective quantum electron transport. These include superconductors, Josephson junctions (JJs) ⁽³⁾, and superconducting quantum computers. ⁽⁴⁾ The latter require milli-Kelvin (mK) temperatures using large dilution refrigerators. Other systems, however, show long-range, collective quantum behaviors at much higher temperatures. High-temperature superconductors and charge density waves ^(5-12) are notable examples.

Coherent tunneling of paired electrons, between two superconductors through an insulating barrier, is a remarkable phenomenon first predicted by Brian Josephson. ⁽³⁾ Two JJs in parallel, each on a branch of a superconducting ring, form a dc SQUID (superconducting quantum interference device). The total critical current of a dc SQUID is a periodic function of magnetic flux. The periodicity is h/2e, where h is Planck’s constant and e is the elementary electric charge.

A related device, the rf SQUID, consists of a single JJ in a superconducting ring, which can couple to a radiofrequency (rf) tank circuit. SQUIDs, embedded within flux-locked loop electronics, create extremely sensitive magnetic sensors. Applications include biomagnetism of the brain, heart, and other organs, geomagnetism, and non-destructive evaluation of conductive materials.

When cooled to mK temperatures, a JJ or SQUID reveals quantized energy levels. ⁽⁴⁾ An rf or dc SQUID forms a flux qubit, while the dc SQUID facilitates tunability of another type of qubit known as the transmon. The transmon consists of a JJ or dc SQUID, with nonlinear kinetic inductance, in parallel with a capacitance. The resulting nonlinear LC circuit leads to quantized energy levels with unequal spacings. The transmon artificial atom is the most widely used qubit in superconducting quantum computers, currently unparalleled in the number of entangled qubits achieved.

The charge density wave (CDW) is a condensate of electrons, coupled to a condensate of lattice vibrations known as phonons, in layered quasi-1D and -2D materials. ^(5-12) CDWs show evidence for collective electron transport above the boiling point of water in some materials, such as NbS3. Early versions of a quantum theory of CDW electron transport were proposed by two-time Nobel laureate John Bardeen ^{(5, 6)} and correlated with experiments by the author, together with John Bardeen and other collaborators. ⁽⁷⁾ Bardeen’s theory was extended into a model of coherent, Josephson-like tunneling, of solitons or paired electrons coupled to phonons, by the author and collaborators. ^(8-11)

The possibility of Josephson-like tunneling of paired electrons, between fluidic electron- and hole-like CDW domain walls, is suggested by several experiments ^{(see 9-11 & cited references)}. These include h/2e-periodic quantum interference in CDW current vs. magnetic flux in NbSe3 crystals with columnar defects and in TaS3 rings.

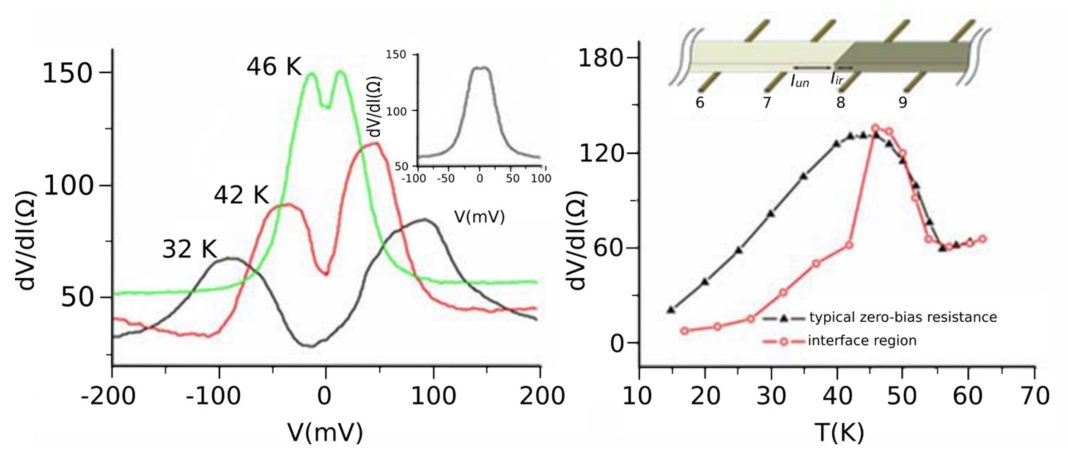
Another intriguing experiment suggests a phase transition, at around 45 K, to an incipient superconducting or superfluid state in a fluidic domain wall near the boundary between boron-implanted and unimplanted regions of NbSe3 ⁽¹²⁾, as shown in Fig. 1.

Quantum computing applications

A potential application of CDWs is quantum reservoir computing to enhance learning speeds of artificial neural networks. ^{(10, 13)}. A more speculative possibility is circuit-based quantum computing, with hybrid CDW-superconductor hybrid devices, at higher-than-mK temperatures. ^{(11, 14)} The development of such applications will require deeper understanding of the underlying quantum behavior of electrons and phonons within the CDW condensate.

References

1. Planck, M. On the law of the energy distribution in the normal spectrum. Ann. Phys. 4, 553 (1901).
2. Kleppner, D. & Jackiw, R. One hundred years of quantum physics. Science 289, 893, 2000.
3. Josephson, B. D. Possible new effects in superconductive tunnelling. Phys. Lett. 1. 251 (1962).
4. Blais, A., Grimsmo, A. L., Girvin, S. M., & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).
5. Bardeen, J. Theory of Non-Ohmic Conduction from Charge-Density Waves in NbSe3. Phys. Rev. Lett. 42, 1498 (1979).
6. Bardeen, J. Tunneling Theory of Charge-Density-Wave Depinning. Phys. Rev. Lett. 45, 1978 (1980).
7. Miller, J. H., Jr., Thorne, R. E., Lyons, W. G., Tucker, J. R., & Bardeen, J. Dynamics of charge-density waves in orthorhombic TaS3. Phys. Rev. B 31, 5229 (1985).
8. Miller, J. H., Jr., Ordóñez, C., & Prodan, E. Time- Correlated Soliton Tunneling in Charge and Spin Density Waves. Phys. Rev. Lett. 84, 1555 (2000).
9. Miller, Jr. J. H., Wijesinghe, A. I., Tang, Z. & Guloy, A. M. Correlated Quantum Transport of Density Wave Electrons. Phys. Rev. Lett. 108, 036404 (2012).
10. Miller, J. H., Jr. & Suárez-Villagrán, M. Y. Quantum fluidic charge density wave transport. Applied Physics Letters 118, 184002 (2021).
11. Miller, J.H., Jr., Suárez-Villagrán, & Sanderson, Johnathan O. Quantum transport of charge density wave electrons in layered materials. Materials Today Physics 41, 101326 (2024).
12. McCarten, J. P., Jones, T. C., Wu, X., Miller, J. H., Jr., Pirtle, I., Xu, X., Claycomb, J. R., Liu, J.-R. & Chu, W.-K. Phase slip scaling relationship for the 59 K and 143 K charge-density-waves in NbSe3. J. Phys. IV France 09, Pr10-129 (1999).
13. Miller, J. H., Jr., Superconductivity and related macroscopic quantum phenomena. Open Access Government, January 2024, pp.244-245. https://doi.org/10.56367/OAG-041-11248
14. Miller, J. H., Villagrán, M. Y. S., Sanderson, J. O. & Wosik, J. Hybrid Quantum Systems for Higher Temperature Quantum Information Processing. IEEE Trans. Appl. Superconductivity 33, 1 (2023).

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.