Kernel tensor decomposition and its use in drug discovery for SARS-CoV-2 was vital, however, due to its general method, it has the potential to be used for a wide range of future problems
Through the series of my previous articles (1-5) that target the general audience, I have been avoiding discussing mathematical details that non-expert cannot easily understand. Nevertheless, I discuss these in this article since it is seemingly the last one about my COVD-19 studies. As a researcher of bioinformatics, my main interest is in the mathematical side. Thus avoiding mathematics has already prevented me from explaining well what I am really interested in.
Kernel tensor decomposition (6), which I am willing to explain here, is an especially difficult concept within my research. This word is composed of two words, kernel and tensor decomposition, respectively, although both are very difficult to understand.
What is Kernel?
Kernel is a nonlinear extension of the inner product computed by multiplying two “vectors” which are lists of real numbers like (1.0,2.0, 3.2, 4.3). The inner sum of two vectors, (1.0,2.0, 3.2, 4.3) and (4.1, 2.0, 3.3, 5.0) can be computed as 1.0×4.1+2.0×2.0+3.2×3.3+4.3×5.0=40.16. The inner product is supposed to measure how two vectors share the same direction, i.e, parallel to each other. Although this is just a mathematical computation, when we add some meaning to vectors, we can compute the similarity between two things. For example, when a vector, (1.0,2.0, 3.2, 4.3), represents the expression of some gene for four persons, the inner product can represent the similarity between the expression of two genes. On the other hand, the kernel is something more advanced. It can measure the similarity of two gene expression profiles not using the inner product but with some function f(x,y) where x and y represent the vectors. f can have a wide range of functions. For example, if f is to be taken as exponential function, kernel between two vectors x and y can be exp[-(x-y)×(x-y)] since it is always positive and is monotonic decreasing function of the distance between x and y, i.e., absolute value of |x-y|.
Explaining tensor decomposition
On the other hand, tensor decomposition (7) is a decomposition of tensors. What is tensor? Tensor is a natural extension of matrix, which is a set of numbers formatted as a form of a Table, e.g.,
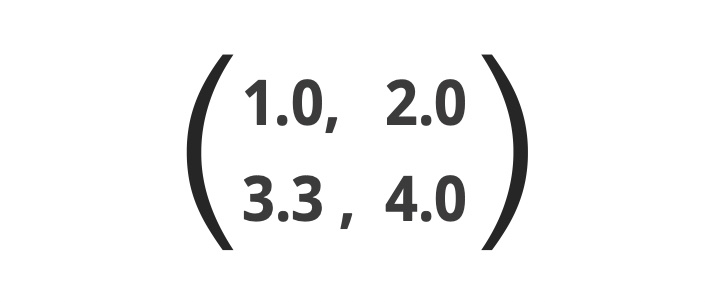
Although matrix has only two indices, i and j and components in matrix can be represented as xij, (e.g, x11=1.0 and x12=2.0), tensor has more than two indices like xijk and it can be decomposed into the product of three vectors, ai, bj, and ck like xijk = ai×bj×ck. This is a tensor decomposition. Again although this is just a mathematical computation, with adding meanings to xijk, e.g, xijk represent the expression of ith gene of jth subject (pearson) in kth tissue (e.g., heart), by decomposing xijk into ai, bj, and ck, we can separately understand the dependence upon i (gene), j (subject) and k (tissue). After that, we can answer the question like “which genes are expressed distinctly between patients and healthy controls in a tissue specific manner? (e.g., only in the heart)” by investigating ai, bj, and ck. The tensor decomposition is known to be performed by applying some mathematical treatments to inner products. With further replacing inner products with advanced kernels and applying the same mathematical treatments to kernel instead of inner product, we can have freedom to select better ai, bj, and ck that can represent more suitable dependence upon i, j, and k.
In actuality, by applying this advanced method called kernel tensor decomposition to gene expression profiles of human lung cell lines that SARS-CoV-2 infected, we could get successfully more accurate set of human genes known to interact with SARS-CoV-2 proteins during infection than those identified with simple (not kernel) tensor decomposition (6). The more suitable set of human genes will result in better drug discovery since the process to find drugs is to find those targeting these identified human genes.
Using kernel tensor decomposition for more
Although we made use of kernel tensor decomposition to drug discovery for SARS-CoV-2, kernel tensor decomposition can be used for a wide range of feature selection problems since it is a general method. Now the method invented for medical purposes started to be used for other purposes because of the methodological generality. This is the essential advantage of a mathematical method; even if the method was invented for a specific purpose, if it is based upon mathematics, the method is able to be applied to others, since vectors, matrices and tensors can represent anything other than something targeted at the initial stage. Math is all.
References
- Y-h. Taguchi, In Silico Drug Discovery for COVID-19 Using an Unsupervised Feature Extraction Method, Scientia, Sep 8, 2021, https://doi.org/10.33548/SCIENTIA727 Sep 8, 2021
- Y-h. Taguchi, How to compete with COVID-19 with a computer? Open Access Government, issue 33, Jan. (2022) pp. 210-211.
- Y-h. Taguchi, Can mice be an effective model animal for Covid-19? Open Access Government, issue 34, April (2022) pp.112-113.
- Y-h. Taguchi, Is human blood better than cell lines as a COVID-19 infection model? Open Access Government, issue 35, July (2022) pp.182-183.
- Y-h. Taguchi, Slight changes can improve much for algorithms looking at gene expressions. Open Access Government, issue 36, October (2022) pp.130-131. https://doi.org/10.56367/OAG-036-10026
- Y-h. Taguchi, and Turki Turki, Mathematical formulation and application of kernel tensor decomposition based unsupervised feature extraction, Knowledge-Based Systems, Volume 217, 2021, 106834. https://doi.org/10.1016/j.knosys.2021.106834
- Y-h. Taguchi, Unsupervised feature extraction applied to bioinformatics, Research Outreach Vol. 115 (2020) pp.154-157. doi:10.32907/ro-115-154157

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.


