Neutrinos, light, matter, and the unification of gravitational and nuclear forces

The discovery of neutrinos and the measurement of their masses are significant events in the history of science. The Rotating Lepton Model provides a useful basis for understanding particles and nuclear reactions, highlighting the importance of Special Relativity, Gravity, and Quantum Mechanics in our universe. Professor Constantinos G. Vayenas explains

The discovery of neutrinos by Pauli some 90 years ago and the measurement of their masses by Kajita and McDonald ⁽¹⁾ some 20 years ago constitute significant developments in the history of science. The recent (2023) ⁽²⁾ detection of neutrino production during the proton-proton collision experiments at CERN confirms the basic assumption of the Rotating Lepton Model (RLM) (2020), ⁽³⁾ i.e. that protons and neutrons comprise rotating neutrino triads, the former with a central positron. This implies that all matter in our Universe, including electromagnetic radiation, ⁽⁴⁾ comprises only five elementary particles: The three neutrinos (ν₁, ν₂, and ν₃), the electron, and the positron. It also implies that two forces (gravity and electromagnetism) suffice for describing the interactions between these five particles and the concomitant production of all other composite particles, such as hadrons and bosons.

Understanding the nature and structure of matter has been a long-sought goal. This subject was already discussed by Plato and his student Aristotle at the Academy of Athens back in the 4^th century BC. They developed two pioneering views, which are both confirmed today via the RLM in an emphatic manner. Thus, Plato writes in his book Timeos: ‘Everything consists of triangles’: (TA ΠΑΝΤΑ ΕΚ ΤΡΙΓΩΝΩΝ ΣΥΝΕΣΤΗΚΕΝ). While Aristotle wrote a few years later in his book Mechanica B, ‘The cause of everything is the cyclic motion’: (ΠΑΝΤΩΝ ΕΧΕΙ ΤΗΣ ΑΙΤΙΑΣ ΤΗΝ ΑΡΧΗΝ Ο ΚΥΚΛΟΣ).

Rotating Lepton Model

As shown from the recent literature ^(3,5,6) and also in this article, both of these brave statements-prognoses of the 4th BC century are in close agreement with the most recent findings on the structure of matter in the interior of atoms as described by the Rotating Lepton Model (RLM) of elementary particles. ⁽⁵⁾

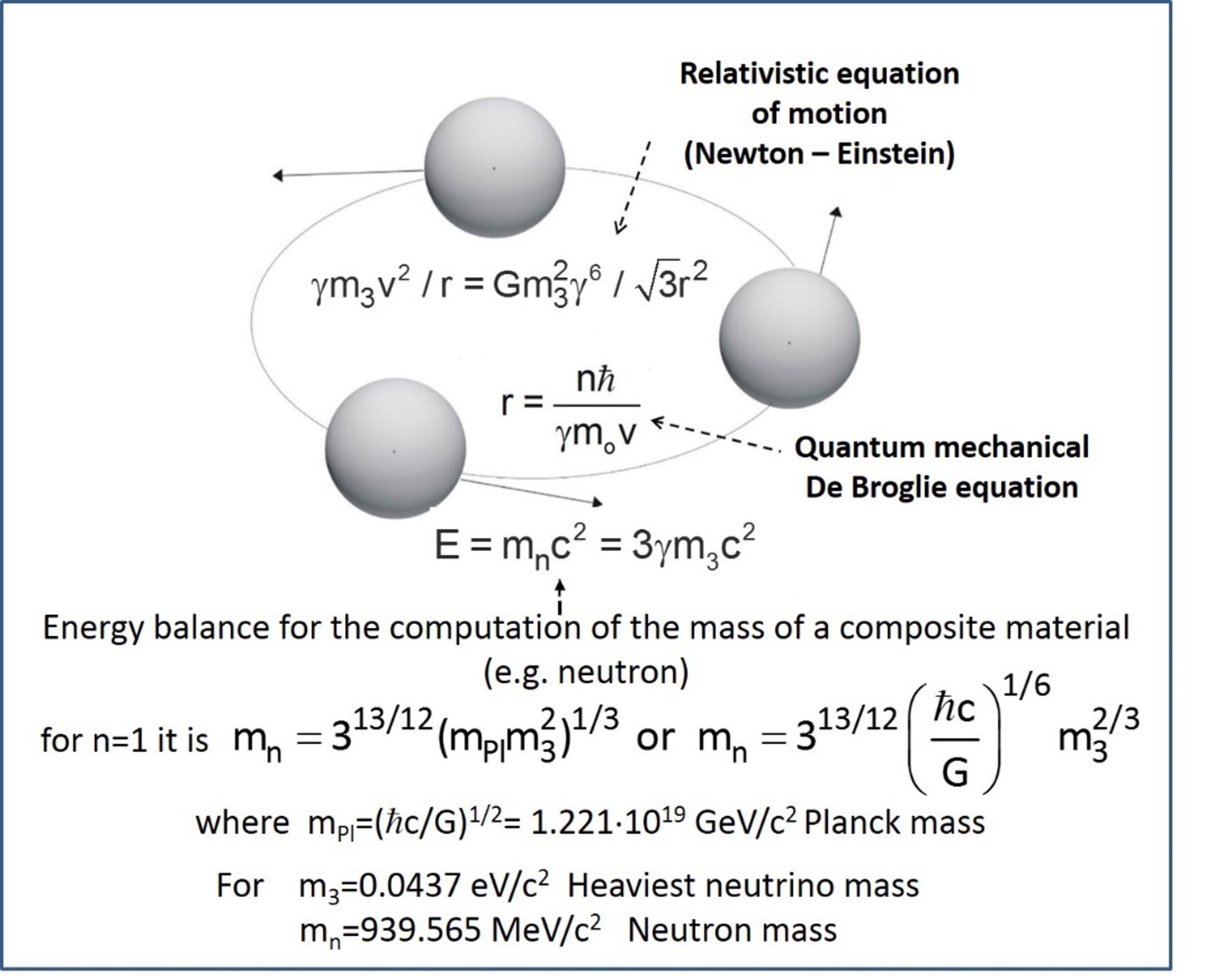
Figure 1 shows the RLM geometry and its two basic equations for a proton or neutron.

Due to their gravitational attraction, the three heavy neutrinos of rest mass m3 each rotate around the center of the triangle they form.

According to the theory of Special Relativity (SR), ^(7,8) the relativistic mass of each of them is γm_o, and the corresponding gravitational mass is γ³m_o where γ = (1-v² / c²)^-1/2 is the Lorentz factor:

Thus, the gravitational force between two rotating neutrinos is given by

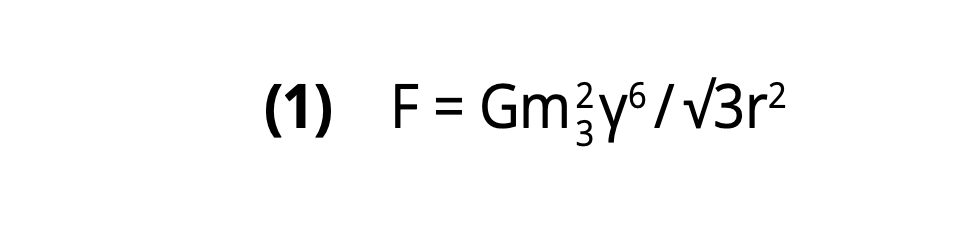
and thus the equation of motion of each rotating particle can be written as:

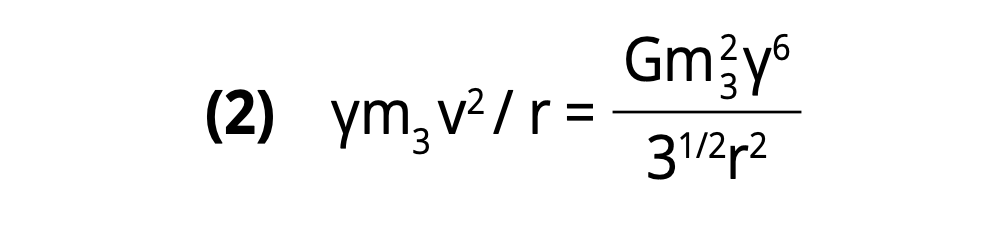
Upon introducing the de Broglie equation ⁽⁹⁾ of quantum mechanics, i.e.

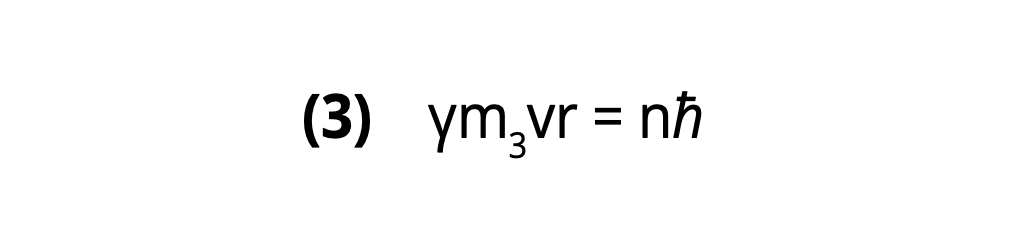
where n is an integer, into equation (2), one obtains from equations (2) and (3)

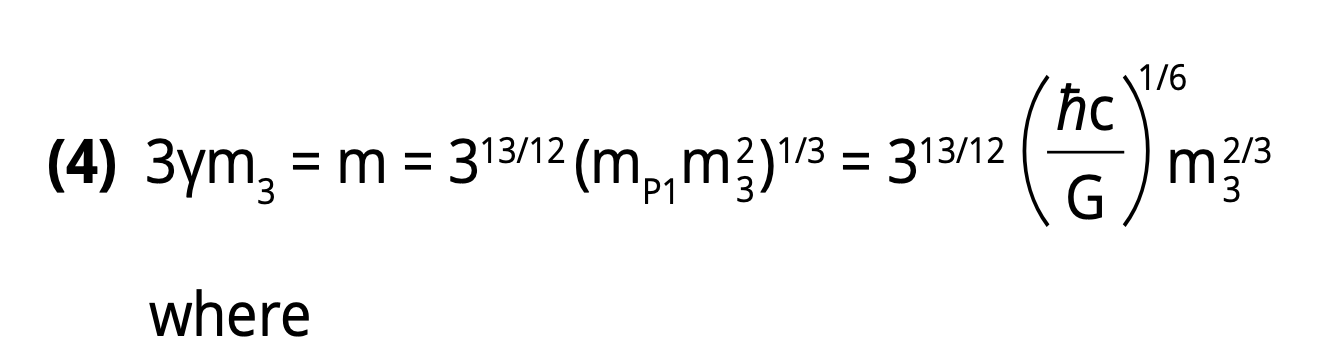
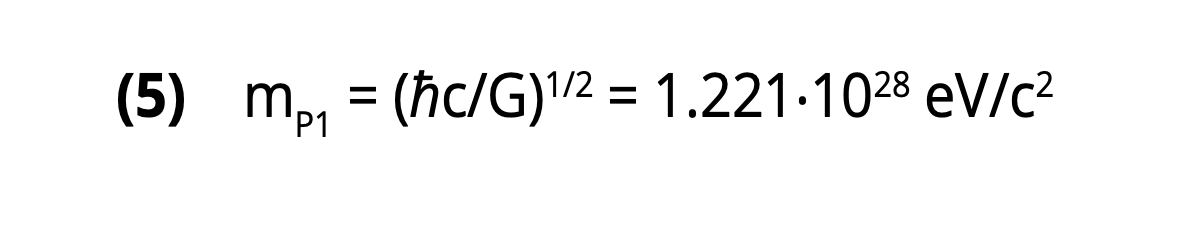
is the Planck mass. For m3=0.0437 eV/c², which is the heaviest neutrino mass, ⁽¹⁰⁾ equation (4) yields

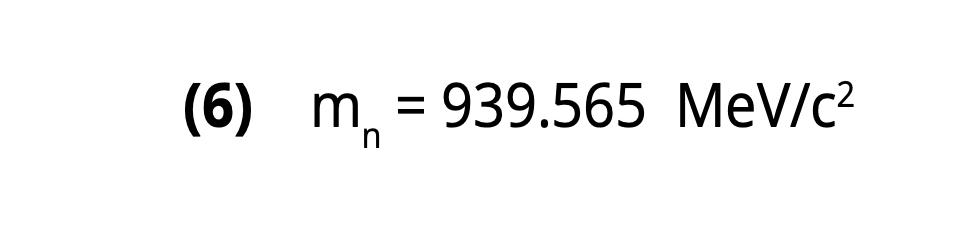
which is the literature value of the neutron mass. ⁽¹¹⁾

The amazing agreement between equation ⁽⁶⁾ and the experimental neutron mass value (Fig. 1) confirms, beyond any reasonable doubt, the validity of the RLM, which has also been used to compute the masses of some twenty-five hadrons and bosons with the same level of agreement between RLM and experiment. ⁽³⁾

This level of agreement between the RLM and the experimental results for the masses of composite particles (protons, neutrons, mesons, and bosons) becomes even more impressive if one takes into account that the RLM does not contain any unknown or adjustable parameters but only uses:

• a. Newton’s gravitational law
• b. Einstein’s theory of Special Relativity (SR)
• c. The simplest equation of quantum mechanics, which describes the quantization of angular momentum.
• d. Energy conservation
• e. The recent experimental
  measurements of the masses of the three neutrinos by Kajita and McDonald ⁽¹⁾ (Nobel Prize in Physics, 2015)

One may wonder why this level of agreement between model and experiment achieved via the RLM in Particle Physics cannot be obtained in Chemistry, where a tedious numerical solution of the Schrödinger equation is inevitable in order to compute the energy levels of atoms. The answer comes from Heisenberg’s uncertainty principle (i.e., ΔpΔr≈ħ). In Physics, the value of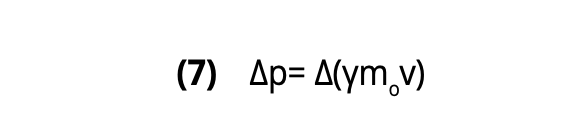

is huge since particle speeds are of the order of c; thus, Δr is very small, while in Chemistry, speeds are barely 1/100 th of c and γ=1, thus leading to at least a hundredfold larger uncertainty in r and the concomitant computed energy levels.

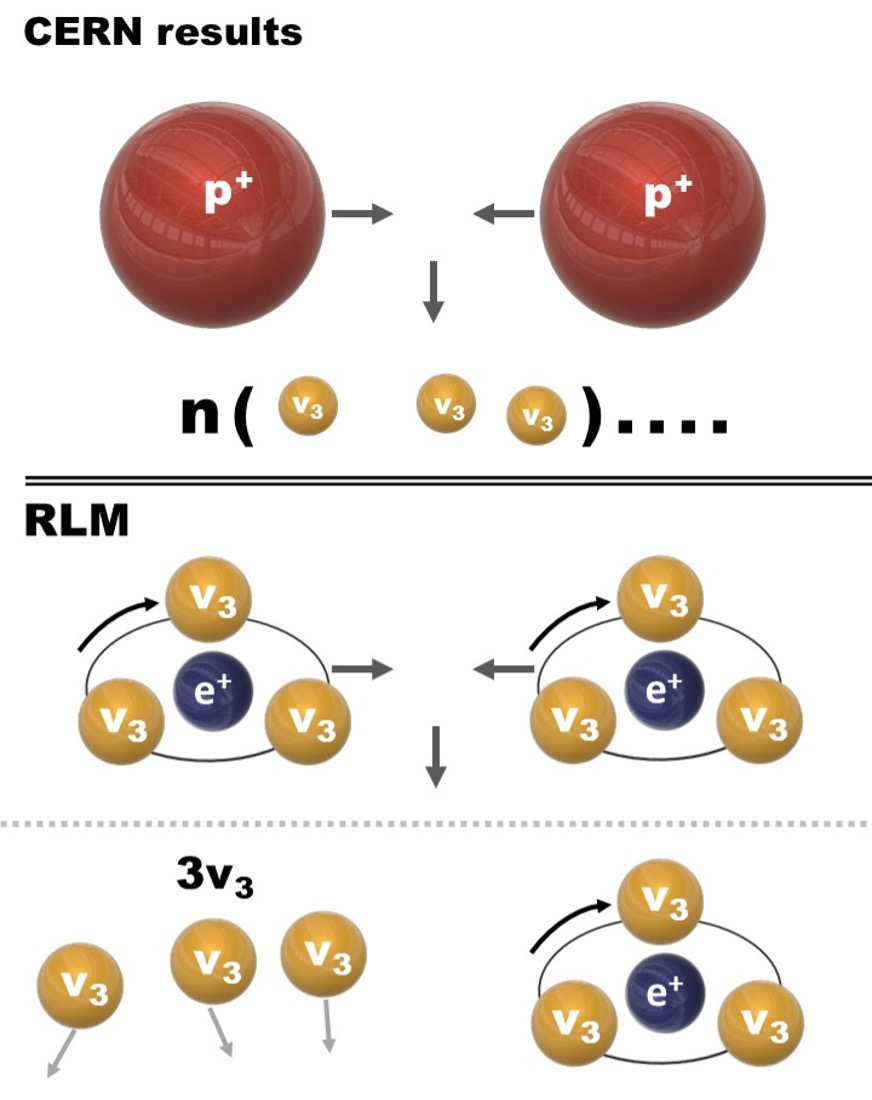
The validity of the RLM was also recently confirmed by the pioneering proton-proton (pp) collisions at CERN ⁽²⁾, which demonstrated that protons contain neutrinos, as shown in Figure 2.

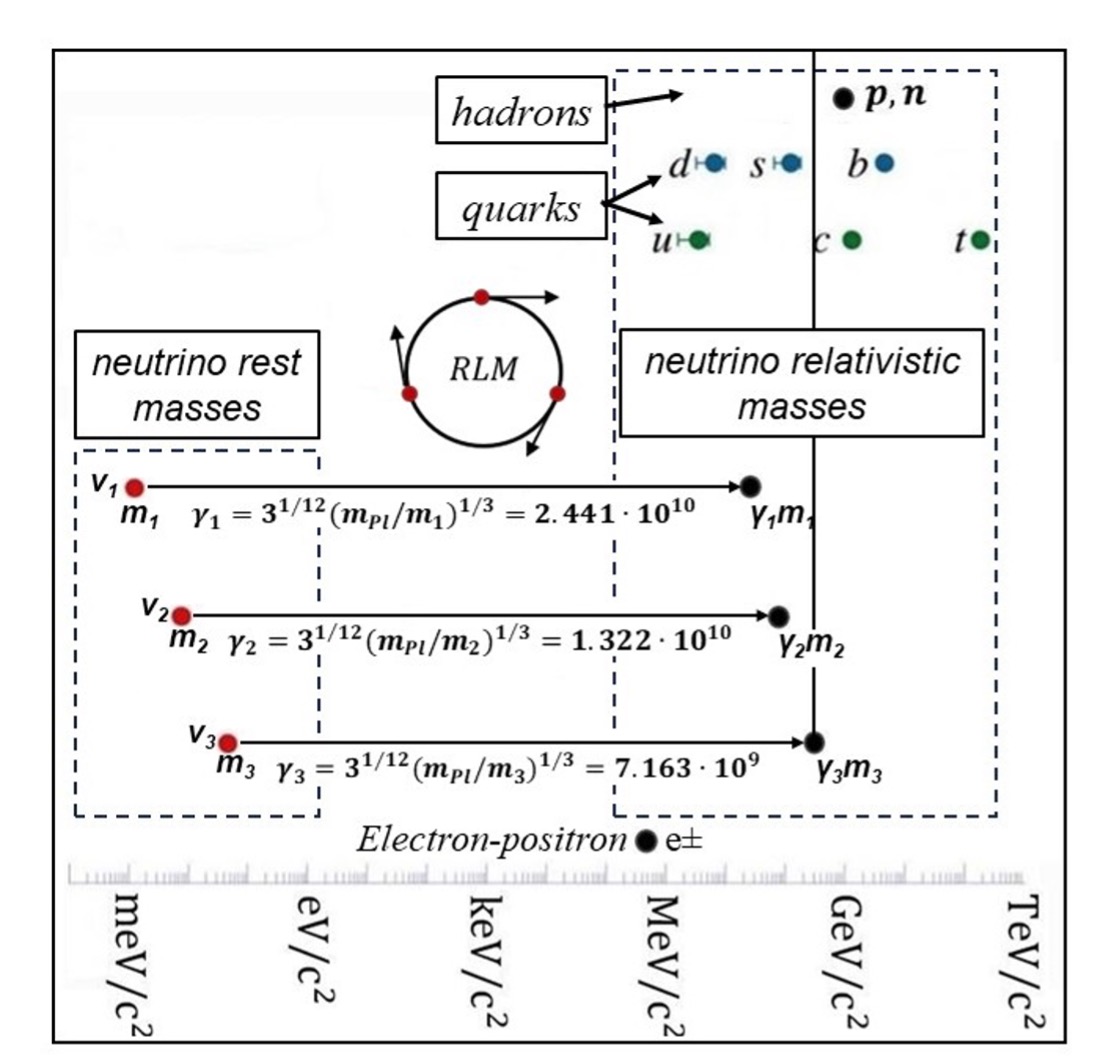
Figure 3 shows the huge gap between the masses of neutrinos and of the hadrons and quarks. How is it thus possible for the extremely light neutrinos (masses of the order of 40 meV/c²) to form quarks and hadrons, which are 100 billion (10¹¹) times heavier? The answer is directly provided by Einstein’s theory of Special Relativity, which dictates that the masses of particles moving close to the speed of light increase dramatically by a factor of γ, which, as shown in Figure 3, is computed via the RLM ⁽³⁾ to be of the order of 10¹⁰, thus bridging the huge mass gap.

The same Figure 3 shows that quarks are rotating relativistic neutrinos. When a hadron decays, then the constituent quarks become immediately very hardly detectable neutrinos. Such neutrinos were nevertheless detected in the pioneering CERN experiments.⁽²⁾

To conclude, the discovery of neutrinos by Pauli and the measurement of their masses by Kajita and McDonald represent very important events in the history of Science and the concomitant effort for the understanding of our Universe. In the same way that the Bohr model established the basis of the molecular understanding of chemical compounds and reactions, the Rotating Lepton Model seems to provide a useful basis for understanding hadrons, bosons, nuclei (e.g., deuteron), and also nuclear reactions. The RLM shows the tremendous importance of Special Relativity, Gravity, and Quantum Mechanics for understanding our Universe.

References

1. Takaaki Kajita, Nobel Lecture (2016): Discovery of Atmospheric Neutrino Oscillations. Rep. Prog. Phys. 69, 1607 – 1635 (2006).
2. Henso Abreu et al, First Direct Observation of Collider Neutrinos with FASER at the LHC, Physical Review Letters (2023).
3. C.G. Vayenas, D. Tsousis, and D. Grigoriou, Computation of the masses, energies and internal pressures of hadrons, mesons, and bosons via the Rotating Lepton Model, Physica A, 545 (2020) 123679.
4. C.G. Vayenas, D. Tsousis, D. Grigoriou. Speeds of Wave Propagation in Ideal Gaseous Molecular and Neutrino Media, J. Phys. Chem. B, 126(23), 4334-4338 (2022).
5. C.G. Vayenas & S. Souentie, Gravity, special relativity and the strong force: A Bohr-Einstein-de-Broglie model for the formation of hadrons. Springer, New York (2012).
6. C.G. Vayenas, S. Souentie, A. Fokas. A Bohr-type model of a composite particle using gravity as the attractive force, Physica A, 405, 360-379 (2014).
7. Einstein A. (1905) Zür Elektrodynamik bewegter Körper. Ann. der Physik., Bd. XVII, S. 17:891-921; English translation On the Electrodynamics of Moving Bodies by G.B. Jeffery and W. Perrett (1923).
8. French AP (1968) Special relativity. W.W. Norton and Co., New York.
9. L.De Broglie,: Waves and Quanta. Nature 112, 540 (1923).
10. C.G. Vayenas, D. Tsousis and D. Grigoriou, Computation of the masses of neutrinos from the Hadron and Boson masses via the Rotating Lepton model of elementary particles. J. Phys.: Conf. Ser. 1730, 012134 (2021).
11. D. Griffiths (2008) Introduction to Elementary Particles. 2nd ed. Wiley-VCH Verlag GmbH & Co. KgaA, Weinheim.

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.