Positron and electron catalysis of neutrino hadronization: How our universe was made

Constantinos G. Vayenas¹, Dionysios Tsousis^1,2 and Eftychia Martino¹, together, discuss how our Universe was made, focusing on positron and electron catalysis of neutrino hadronization

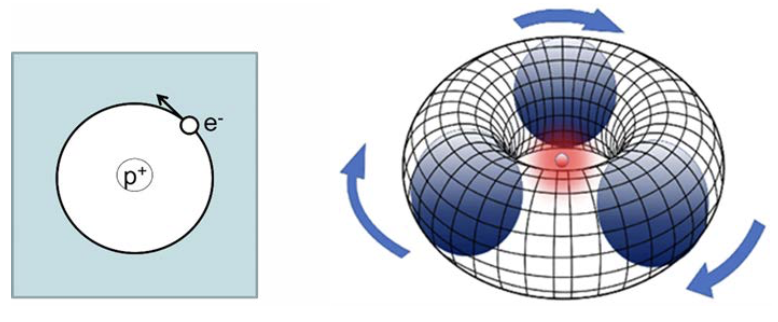
The development of the Bohr model for the H atom (Fig. 1) has played a central role in reaching our current level of understanding of chemical synthesis.

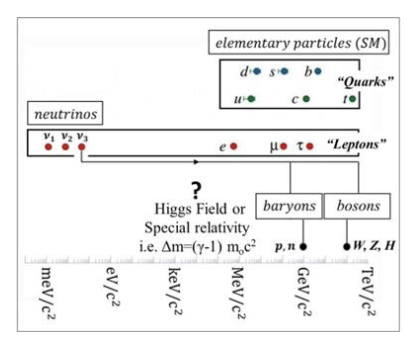
In recent years, the development of the Rotating Lepton Model (RLM) of hadrons and bosons ^(1-4) provided an equally effective approach for modeling the structure and accurately computing the masses of subatomic particles, such as hadrons and bosons, nuclei and even cosmic rays. ⁽⁴⁾

The RLM bears an important similarity with the Bohr model of the H atom, i.e., it comprises one or more rotating leptons on a circular orbit, gravitationally attracting themselves and not electrostatically as is the case of the Bohr model. In the case of the RLM, the rotating leptons are mostly neutrinos, which have extremely small (~1-5 eV/c²) rest masses. However, due to their lightness, these rotating neutrinos easily reach highly relativistic speeds, extremely close to the speed of light.

Thus, according to Einstein’s Special Relativity, their relativistic and gravitational masses of γm_o and γ³m_o, respectively, increase dramatically and reach values of the order of 109 eV/c2 and 10²⁸ eV/c², respectively. This implies that the intraparticle gravitational forces reach the Strong Force value of ћc/r², which is 10³⁰ times stronger than the normal gravitational attraction at the same distance.

The mechanism of hadronization (or baryogenesis)

Careful examination of the decay products of several hundreds of composite particles, such as of hadrons (including baryons and mesons) ^{(4, 7-8)} has shown that the ultimate decay products of all composite particles are only the following five leptons: The electron (e^–), the positron (e⁺) and the three neutrinos (ν₁, ν₂ and ν₃), the masses of which were first measured by Kajita ⁽⁹⁾ and McDonald ⁽¹⁰⁾ in their pioneering work. These masses are of the order of 3 to 50 meV/c², i.e., 12 orders of magnitude (a million million times) smaller than the masses of protons/neutrons (10⁹ eV/c²).

A first question arising from these extremely demanding to measure and dramatically different mass values of neutrinos vs those of the basic constituents of atoms (i.e., protons, neutrons and electrons) is how the tiny masses of neutrinos are related to the huge (by neutrino standards) masses of our familiar electrons and protons which are typically 11 orders of magnitude bigger than those of neutrinos.

The answer to this question is obtained by the ingenious 1905 masterpiece of Einstein, i.e., by Special Relativity, which, in simple words, dictates that what is really important in this world is not what we measure about ourselves but instead what the others observe about us.

Thus, the measured relativistic mass, γm_o, of a particle, e.g., a neutrino, of rest mass m_o, travelling with a Lorentz factor of 10¹⁰ is of the order of 10⁹ eV/c², i.e., 1 GeV/c², i.e., of the order of proton and neutron masses. ⁽¹¹⁾ At the same time, its gravitational mass, γ³m_o ⁽⁵⁾ reaches the Planck mass. ^(1-4). This provides the key idea of the Rotating Lepton Model (RLM) of composite particles which is a simple Bohr-type model of three gravitating rotating neutrinos moving with speeds very close to the speed of light. ^(1-4) This appears to be how the matter of our Universe has been made (or is being made even today according to the pioneering CERN experiments). ⁽¹²⁾

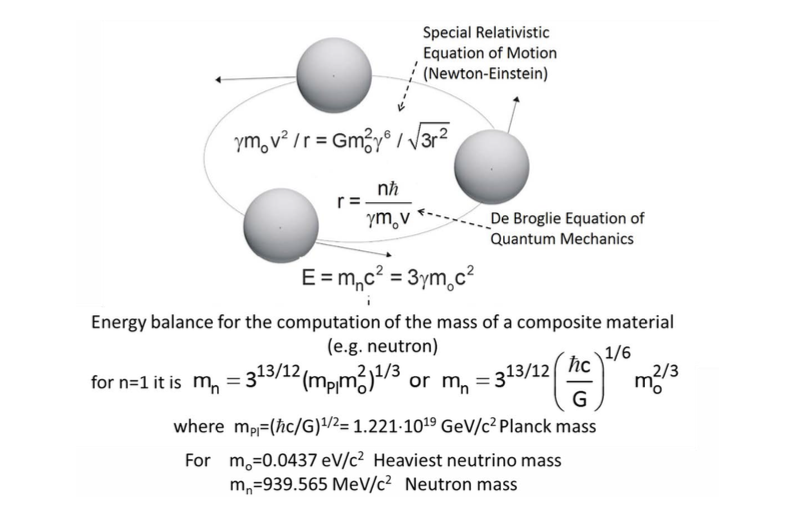
The three basic equations of the RLM are given in Figure 2. They represent Newton’s gravitational Law coupled with Einstein’s special relativity and with the de Broglie equation of quantum mechanics.

In addition to these three scientific giants, there are two more exceptional scientists – philosophers who are worth mentioning, i.e., Plato with his famous phrase “Everything consists of triangles” and his student Aristotle with his equally prophetic “The cyclic motion is the origin of everything”, both exactly confirmed today by the RLM geometry.

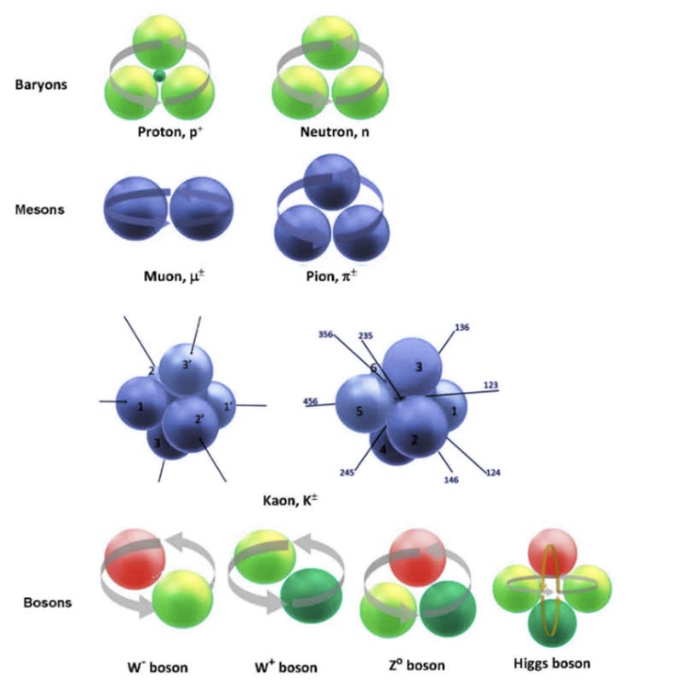
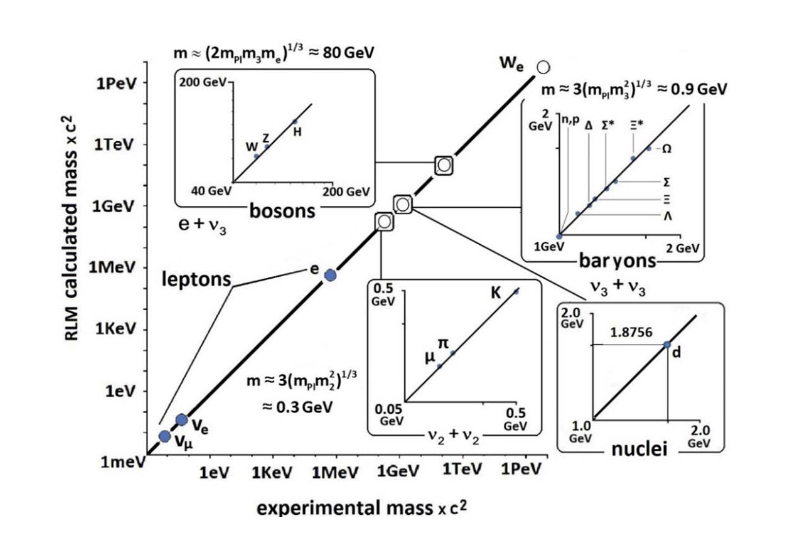
Figure 3 shows the geometries of the most common hadrons and bosons used to compute their masses via the RLM, while Figure 4 compares these computed masses with the experimental ones. ⁽⁴⁾ Agreement is typically better than 2%.

Gravitational catalysis

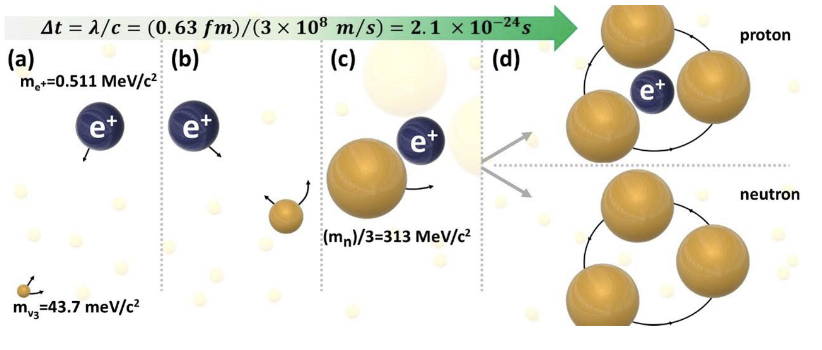
A basic question since the conception of the RLM is how the neutrinos reach or have reached the highly relativistic speeds which, via Einstein’s special relativity ⁽⁵⁾, bring their masses from rest masses (~10^-2 eV/c²) ^(4,13) to the highly relativistic masses (~10⁹ eV/c²) of those rotating in protons and neutrons. ⁽⁴⁾ The answer has been provided by some recent works ^(1-4), as shown in Figure 5. It results from an initial catalytic gravitational acceleration of neutrinos by positrons (and/or) electrons to highly relativistic velocities followed by the steady-state gravitational attraction by the other co-rotating neutrinos (Fig. 6). This two-step gravitational catalysis concept appears to be quite effective. ⁽⁴⁾

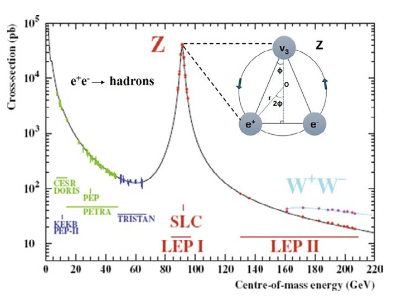
The validity of the RLM is confirmed emphatically from a recent important and, until recently, unexplained CERN experiment, shown in Figure 7, in which positrons and electrons are cofed in a “vacuum” chamber which, unavoidably, contains trillions of neutrinos. Thus, the Z boson peak in Figure 7 can be immediately understood by the fact that, as shown recently ⁽¹³⁾, the Z boson is a rotating electron-positron-neutrino structure.

Authors

1. University of Patras
2. Stanford University

References

1. C.G. Vayenas & S. Souentie, Gravity, special relativity and the strong force: A Bohr-Einstein-de-Broglie model for the formation of hadrons. Springer, New York (2012).
2. C.G. Vayenas, S. Souentie, A. Fokas. A Bohr-type model of a composite particle using gravity as the attractive force, Physica A, 405, 360-379 (2014).
3. C.G. Vayenas, D. Tsousis and D. Grigoriou, Computation of the masses, energies and internal pressures of hadrons, mesons and bosons via the Rotating Lepton Model, Physica A, 545 (2020) 123679.
4. C.G. Vayenas, D.G. Tsousis, E.H. Martino, “Catalysis in Chemistry and Physics: The Roles of Leptons, Special Relativity and Quantum Mechanics”, Springer Nature, Switzerland AG, (2024). ISBN978-3-031-68121-9.
5. A. Einstein (1905) Zür Elektrodynamik bewegter Körper. Ann. der Physik., Bd. XVII, S. 17:891-921; English translation On the Electrodynamics of Moving Bodies (http://fourmilab.ch/etexts/einstein/specrel/www/) by G.B. Jeffery and W. Perrett (1923).
6. A.P. French (1968) Special relativity. W.W. Norton and Co., New York.
7. R.L. Workman et al. (Particle Data Group) (2022) The review of particle physics. Prog. Theor. Exp. Phys., 083C01 (2022).
8. The Rotating Lepton Model: Electron and Positron Catalysis of Chemical and Nuclear synthesis, Open Access Government, October 2023.
9. Takaaki Kajita, Nobel Lecture (2016): Discovery of Atmospheric Neutrino Oscillations. Rep. Prog. Phys. 69, 1607 – 1635 (2006).
10. A.B. McDonald, Nobel Lecture: The Sudbury Neutrino Observatory: Observation of flavor change for solar neutrinos. Rev. Mod. Phys. 88, 030502 (1-9) (2016).
11. D. Griffiths (2008) Introduction to Elementary Particles. 2nd ed. Wiley-VCH. Verlag GmbH & Co. KgaA, Weinheim.
12. Precision electroweak measurements on the Z resonance, Physics Reports, 427, (5–6), 257-454, 2006, https://doi.org/10.1016/j.physrep.2005.12.006
13. A.S. Fokas, C.G. Vayenas. On the structure, mass and thermodynamics of the Zo bosons. Physica A, 464, 231-240 (2016).