The rotating lepton model: Electron and positron catalysis of chemical and nuclear synthesis

Professor Emeritus Constantinos Vayenas from the University of Patras and PhD student Dionysios Tsousis from Stanford University discuss electron and positron catalysis in the CERN e⁺e^– annihilation experiments via the Rotating Lepton Model

Electrons and positrons play a central role in heterogeneous catalysis ^(1,2) and electrochemistry ^(3,4) since they can interact directly via electrostatic interactions with molecular or ionic reactants, intermediates, and products. Electrochemistry’s entire science and technology is based on electrostatic electron – or positron-atom interactions.

Interestingly, it has also been known for some years from the positron-electron annihilation experiments ⁽⁵⁾ that beams of electrons and positrons can produce significant amounts of a variety of hadronic particles ^(5,6), hadrons and bosons “in a vacuum”.

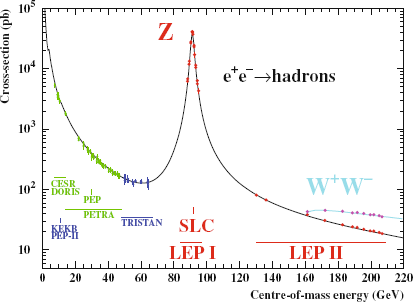
The mechanism of this startling behaviour has been unclear for many years. One might initially argue that the energy released from the exothermic positron-electron neutralisation is somehow converted to the masses of the plethora of products observed, among which the Z boson is the dominant product (Figure 1). However, no physical mechanism is known for producing hadrons and bosons from energy alone.

The elementary particles

Careful examination of the decay products of all known particles reveals that the ultimate final dissociation products of all known composite particles are only five, i.e., the positron, the electron and the three neutrinos with masses m₁, m₂, and m₃. ^(7,8,9) These are the only real elementary (“atomic” in the Democritian sense) particles. Neutrinos are also commonly classified in terms of their “flavor”, i.e., e-neutrinos, μ-neutrinos and τ-neutrinos, depending on the particle (e, μ or τ) appearing with them upon detection.

The reason for this simultaneous emergence is discussed in the last section. However, as shown recently and analysed here based on the structure of hadrons and bosons revealed by the Rotating Lepton Model (RLM) ^(9,10,11), the fundamental neutrino classification in terms of their masses (i.e. ν₁, ν₂ and ν₃) is more fundamental rather than that according to their “flavors”.

Microscopic reversibility and the Rotating Lepton Model

Since a combination of neutrinos, positrons, and electrons is the final product of the dissociation of all composite particles (hadrons, bosons), it follows from the principle of microscopic reversibility that all composite particles can be constructed by combining positrons, electrons, and neutrinos.

There is a critical difficulty with this simple view having to do with the range of masses of neutrinos (10^-3 to 10^-1 eV/c²), hadrons (1 to 10 GeV/c²) and bosons (80-120 GeV/c²) (Fig. 2) and with the fact that quarks are commonly perceived to be the components of hadrons.

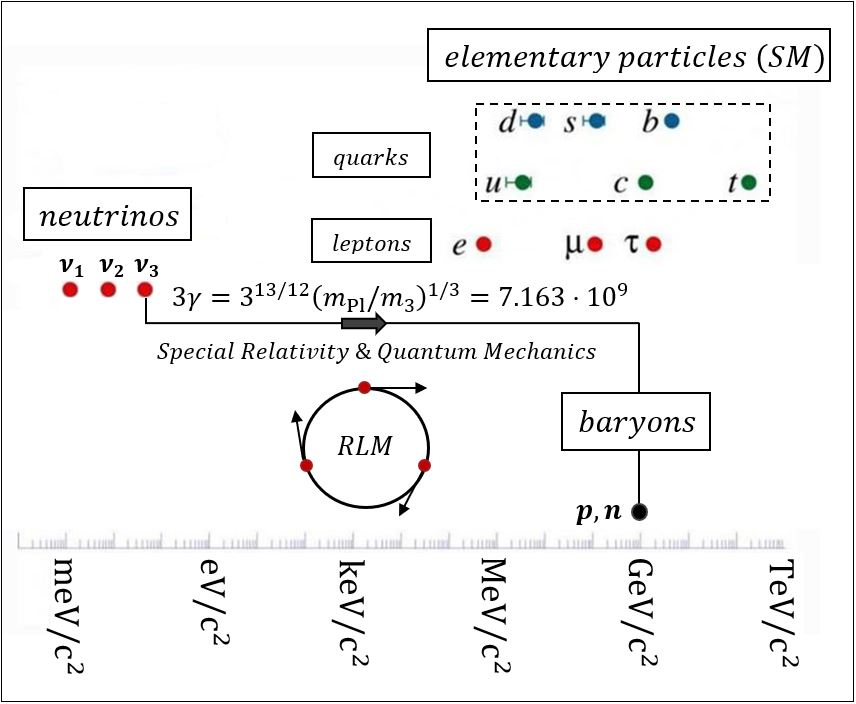
As shown in Figure 2, Special Relativity, a basic component of the Rotating Lepton Model (RLM), directly solves this problem. In the RLM, hadrons, such as the neutron, are modelled as a triad of ultrafast relativistic gravitating neutrinos. The tremendous speeds
(γ ≈ 10^{10 (9,10,11)}) reached by the three rotating neutrinos cause their masses to increase (from ~10^-2 eV/c²) by a factor of γ.

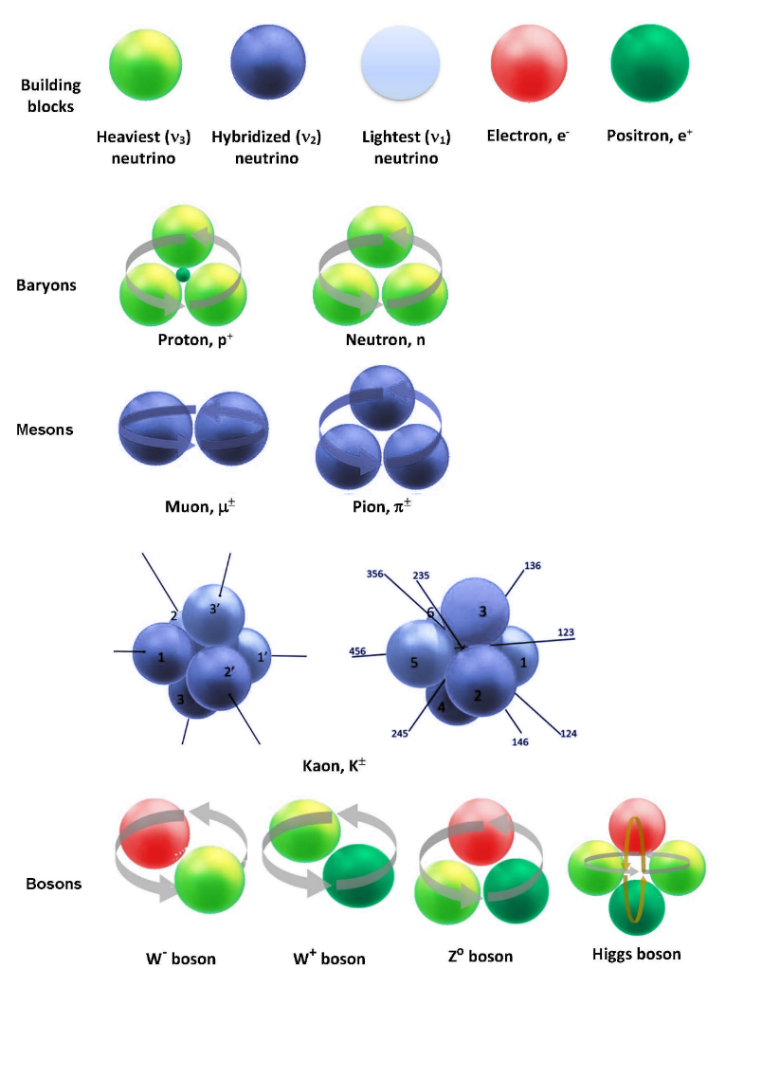
Thus, surprisingly, the neutrino masses reach the values of the quark masses, and, in this way, the masses of hadrons (baryons) are obtained (~1 GeV/c²), which are ten orders of magnitude heavier than those of neutrinos. In this way, the RLM provides a quantitative fit to the masses of hadrons and the masses of bosons (such as the Z, W and Higgs bosons) which contain a rotating electron in their rotating ring (Fig. 3).

Experimental validations of the RLM

The positron-electron annihilation (PEA) experiments carried out at CERN ⁽⁷⁾ provide direct proof of the validity of the RLM. As shown in Figure 1, the main product of the PEA is the Z boson. The RLM has already demonstrated this to comprise a rotating positron- electron-neutrino triad ⁽¹²⁾ (Fig 3). Furthermore, the computed via the RLM mass m_Z=(m_Plm_em_ν)^1/3≈92 GeV/c² is in quantitative agreement with the location of the Z peak (Fig. 1).

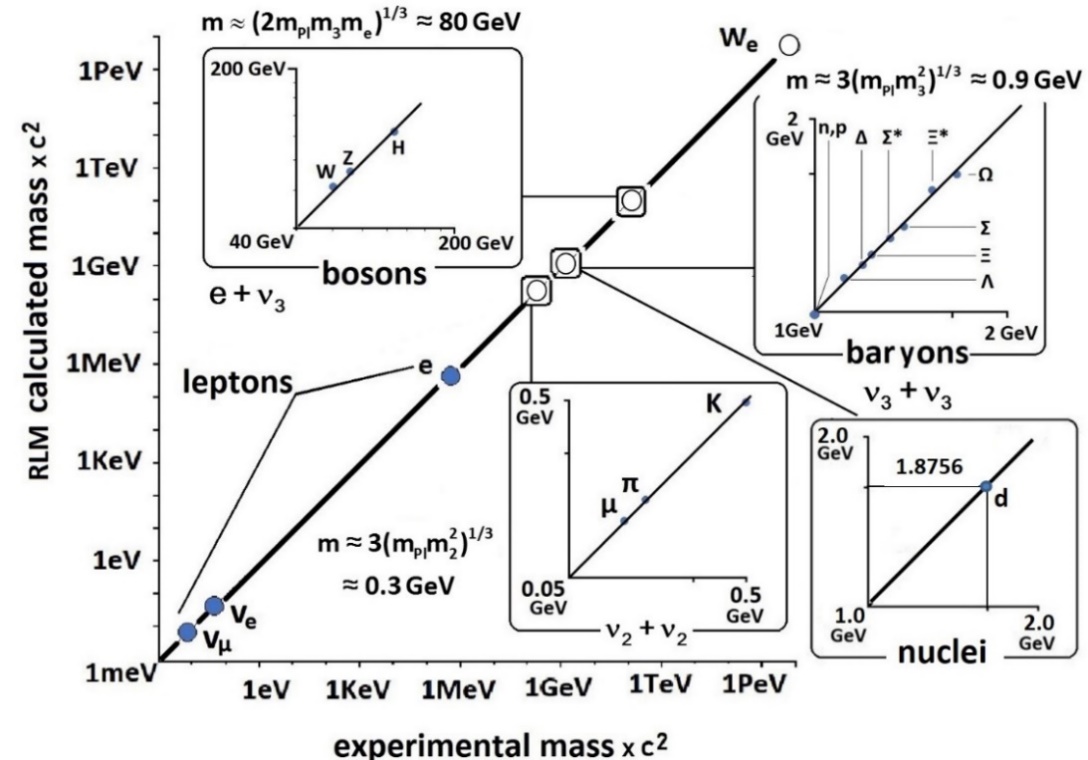
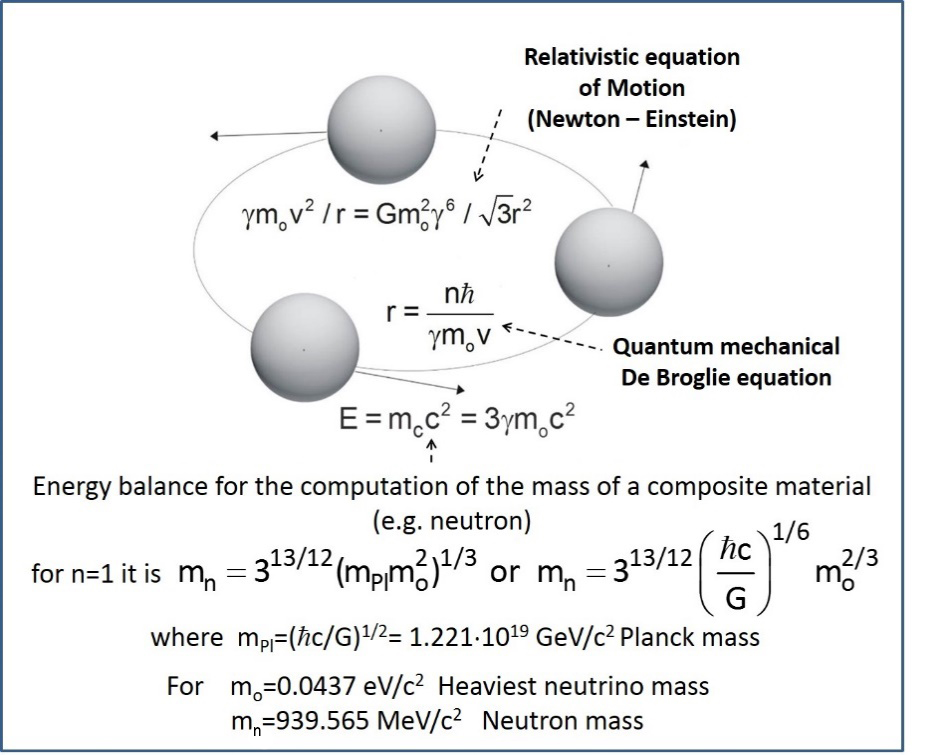
A thorough validation of the RLM for a total of 25 composite particles (hadrons), including the proton, the neutron, bosons, and the deuteron nucleus (11), is shown in Figure 4. As shown in this Figure, all the corresponding points fall (within 2%) on the y=x line. The agreement is also quantitative. Figure 5 presents the RLM methodology. It comprises only three equations:

1. The equation of motion which accounts for special relativity via the relativistic masses, γmo, and utilises the gravitational particle masses in Newton’s gravitational law. Gravitational masses are equal to inertial masses according to the equivalence principle, i.e., are equal to γ³m_o where γ(=(1-v²/c²) ^-1/2) is the Lorentz factor.

2. The de Broglie wavelength equation which states that each particle’s angular momentum, γm_ovr, equals the Planck constant ħ. There are only two unknowns in these two equations, i.e., γ and r, the radius. The solution of these equations together with the energy balance equation of fig.5 gives:

(1)

and thus

(2) For m_o=0.0437 eV/c2 (within the mass range measured at Superkamiokande), this gives the experimental neutron mass of 939.565 MeV/c2.

Neutrino rest masses computation

Conversely, one may rewrite equation (2) as:
(3)
This allows for the computation of the heaviest neutrino mass, m3, which agrees with the value obtained at the Superkamiokande facility. (13)

Structural information

Figures 3,4, and 5 underline the usefulness and importance of the RLM. They also show that:

(a). Bosons contain rotating electrons in their structure, and this leads to their significantly larger (by a factor of (m_e/m_ν3)1/3=10²) values of boson masses vs hadron masses.

(b). The Z boson is a rotating e⁺-e^— ν3 triad, and this explains why it is the dominant product of the PEA experiments formed by the interaction of e+-e– pairs with ambient neutrinos.

(c). From the structure of the W boson (i.e. a rotating e⁺-ν₃ pair), it follows why an electron (or positron) is always appearing simultaneously with each observed ν₃ neutrino.

In summary, the CERN positron-electron annihilation experiments shed new light on the interactions between neutrinos, positrons and electrons and confirm the mechanism of the Rotating Lepton Model by showing that the Z boson is a rotating positron-electron-neutrino (m₃) (e⁺e– ν₃) particle.

The neutrino in the Z boson structure is already rotating at a tremendous speed. Thus, upon Z boson decomposition, it can accelerate many more neutrinos to highly relativity speeds, thus further catalysing hadronization.

Z boson-type bosons can also form via the interaction of electrons with ambient m₂ and m₁ type neutrinos, and this explains why each electron neutrino (which comprises a mixture of e–ν₁, e–ν₂ and e–ν₃ bosons) has an average mass between those corresponding to m₁, m₂ and m₃ type neutrinos. This appears to clarify the neutrino-flavor concept, i.e., an electron neutrino has emerged via the dissociation of a W boson. In contrast, a muon neutrino is the result of the dissociation of a pion complex, and a tau neutrino is the dissociation product of a tau-neutrino complex.

References

1.  L. Pauling, The Nature of the Chemical Bond (3rd ed., Oxford University Press 1960) p. 111-120.
2. G. Ertl, H. Knözinger, F. Schüth (Eds.) in Handbook of Heterogeneous Catalysis, 2nd Ed., Vol. 1, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim (2008).
3. J. O’ M. Bockris & A.K.N. Reddy, Modern Electrochemistry 1, 2nd ed., Plenum Press, New York, (1998).
4. C.G. Vayenas, S. Bebelis, C. Pliangos, S. Brosda, and D. Tsiplakides, “Electrochemical Activation of Catalysis: Promotion, Electrochemical Promotion and Metal-Support Interactions” Kluwer/Plenum Press, New York (2001).
5. A. Straessner, Electroweak Physics at LEP and LHC, Springer (2010).
6. Workman RL et al. (Particle Data Group) (2022) The review of particle physics. Prog. Theor. Exp. Phys 2022:083C01.
7.  C.G. Vayenas and D.G. Tsousis, “The catalytic role of Electrons and Positrons in the synthesis of Chemicals and of Hadrons”, Topics in Catalysis, (2023) https://doi.org/10.1007/s11244-023-01812-9.
8. C.G. Vayenas, S. N.-A. Souentie, Gravity, special relativity and the strong force: A Bohr-Einstein-de Broglie model for the formation of hadrons. (Springer, NY, 2012).
9. C.G. Vayenas, D. Tsousis and D. Grigoriou, “Computation of the masses, energies and internal pressures of hadrons, mesons and bosons via the Rotating Lepton Model”, Physica A, 545 (2020) 123679.
10. C.G. Vayenas, D. Grigoriou, D. Tsousis, K. Parisis and E.C. Aifantis, “Computation of the deuteron mass and force unification via the Rotating Lepton Model”, Axioms 11, 657 (2022).
11. A.S. Fokas, C.G. Vayenas, “On the structure, mass and thermodynamics of the Zo bosons”. Physica A, 464, 231- 240 (2016).
12. T. Kajita, Discovery of neutrino oscillations. Rep. Prog. Phys. 2006, 69, 1607–1635.
13. C.G. Vayenas, D. Tsousis and D. Grigoriou, “Computation of the masses of neutrinos from the Hadron and Boson masses via the Rotating Lepton model of elementary
    particles” J. Phys.: Conf. Ser. 1730, 012134 (2021).

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.