Search for long-range magnetic order in quasicrystals

Zbigniew M. Stadnik, Professor at the University of Ottawa in the Department of Physics, looks at the magnetic order in quasicrystals

Classification of solids is based upon the order and rotational symmetry of their atomic arrangements. Until 1984, solids were either crystalline or amorphous. In crystalline compounds, atoms or atomic clusters are ordered periodically (in a repeating pattern), and the rotational symmetries of such compounds are restricted to two-, three-, four-, and six-fold symmetry axes. Thus, five-fold or 10-fold symmetry axes, for instance, are forbidden. In amorphous compounds, the atomic arrangements are essentially disordered with no precise rotational symmetry.

Quasiperiodic order might lead to unusual physical properties

Quasicrystals (QCs), short for quasiperiodic crystals [1], discovered in 1984 by Daniel Shechtman [2] in the Al-Mn alloys (the 2011 Nobel Prize in Chemistry), belong to the new, third group of solids where the atomic arrangements are still ordered, but the pattern is not periodic, i.e., it does not repeat (quasiperiodic order). Currently known QCs possess five- fold, eight-fold, 10-fold, and 12-fold symmetry axes [3].

Soon after the discovery of QCs, it was speculated that quasiperiodic order might lead to unusual physical properties that do not occur in crystalline or amorphous compounds. Such unusual and specific to QCs, physical properties have not yet been found. Instead, with one notable exception discussed below, the same physical phenomena as those occurring in crystalline or amorphous compounds were also observed in QCs. Thus, for example, such phenomena as diamagnetism [4], paramagnetism [5], spin-glass [6], or superconductivity [7] were found in some QCs.

Until very recently, no long-range magnetic order was found in QCs

The claim of the discovery of the existence of long-range magnetic order in icosahedral RE-Mg-Zn (RE=rare earth) QCs [8] was shown [9] to result from the presence of magnetic impurities in the samples studied. Initial intuition suggests that quasiperiodicity necessarily leads to geometrical frustration and is therefore incompatible with long-range magnetic order. However, numerous theoretical studies [10-12] have established that long-range magnetic order on a quasilattice is entirely possible.

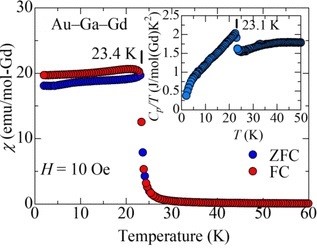
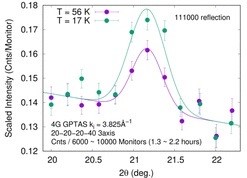
The experimental breakthrough occurred in 2021 when the presence of long-range magnetic order was convincingly determined in the icosahedral Au₆₅Ga₂₀Gd₁₅ QC and possibly also in the icosahedral Au₆₅Ga₂₀Gd₁₅ QC [13].The temperature dependence of magnetic susceptibility, χ, of the icosahedral Au₆₅Ga₂₀Gd₁₅ QC suggests a ferromagnetic transition at 23.4 K. This transition is confirmed by the presence of the λ-shaped anomaly in the specific heat, C_p, at 23.1 K. These χ(T) and C_p (T) dependencies indicate that the icosahedral Au₆₅Ga₂₀Gd₁₅ QC is a ferromagnet with a Curie temperature T_c = 23 K. The ferromagnetic long-range magnetic order in the icosahedral Au₆₅Ga₂₀Gd₁₅ QC is confirmed by neutron diffraction experiments carried out at temperatures below and above T_c. One observes that the 111000 reflection intensity increases at 17 K (below T_c) where ferromagnetic order is established, compared to that at 56 K (above T_c).

Similar χ(T), C_p(T), and neutron diffraction experiments on the icosahedral Au₆₅Ga₂₀Gd₁₅ QC seem to establish that this QC is also a ferromagnet with T_c = 16 K [13].

To summarise, after a long search for QCs with long-range magnetic order, we now know two ferromagnets, icosahedral Au₆₅Ga₂₀Gd₁₅and Au₆₅Ga₂₀Gd₁₅ QCs, with Curie temperatures of 23 and 16 K, respectively.

References

1. D. Levine and P.J. Steinhardt, Phys. Rev. Lett. 53, 2477 (1984).
2. D. Shechtman, I. Blech, D. Gratias, and J.W. Cahn, Phys. Rev. Lett. 53, 1951 (1984).
3. Physical Properties of Quasicrystals, edited by Z.M. Stadnik (Springer-Verlag, Berlin, 1999).
4. C.R. Lin, S.T. Lin, C.R. Wang, S.L. Chou, H.E. Horng, J.M. Cheng, Y.D. Yao, and S.C. Lai, J. Phys.: Condens. Matter 9, 1509 (1997).
5. Z.M. Stadnik and P. Wang, J. Phys.: Condens. Matter 18, 8383 (2006).
6. K. Al-Qadi, P. Wang, Z.M. Stadnik, and J. Przewoźnik, Phys. Rev. B79, 224202 (2009).
7. K. Kamiya, T. Takeuchi, N. Kabeya, N. Wada, T. Ishimasa, A. Ochiai, K. Deguchi, K. Imura, and N.K. Sato, Nature Commun. 9, 154 (2018).
8. B. Charrier, B. Ouladdiaf, and D. Schmitt, Phys. Rev. Lett. 78, 4637 (1997).
9. Z. Islam, I.R. Fisher, J. Zarestky, P.C. Canfield, C. Stassis, and A.I. Goldman, Phys. Rev. B57, R11047 (1998).
10. Z.M. Stadnik, in Handbook of Magnetic Materials, Vol. 22, edited by K.H.J. Buschow (Elsevier, Amsterdam, 2013), p. 77, and references therein.
11. S. Thiem and J.T. Chalker, Phys. Rev. B92, 224409 (2015).
12. S. Watanabe, Proc. Natl. Acad. Sci. USA 118, e2112202118 (2021).
13. R. Tamura, A. Ishikawa, S. Suzuki, T. Kotajima, Y. Tanaka, T. Seki, N. Shibata, T. Yamada, T. Fujii, C-W. Wang, M. Avdeev, K. Nawa, D. Okuyama, and T.J. Sato, J. Am. Chem. Soc. 143, 19938 (2021).

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.