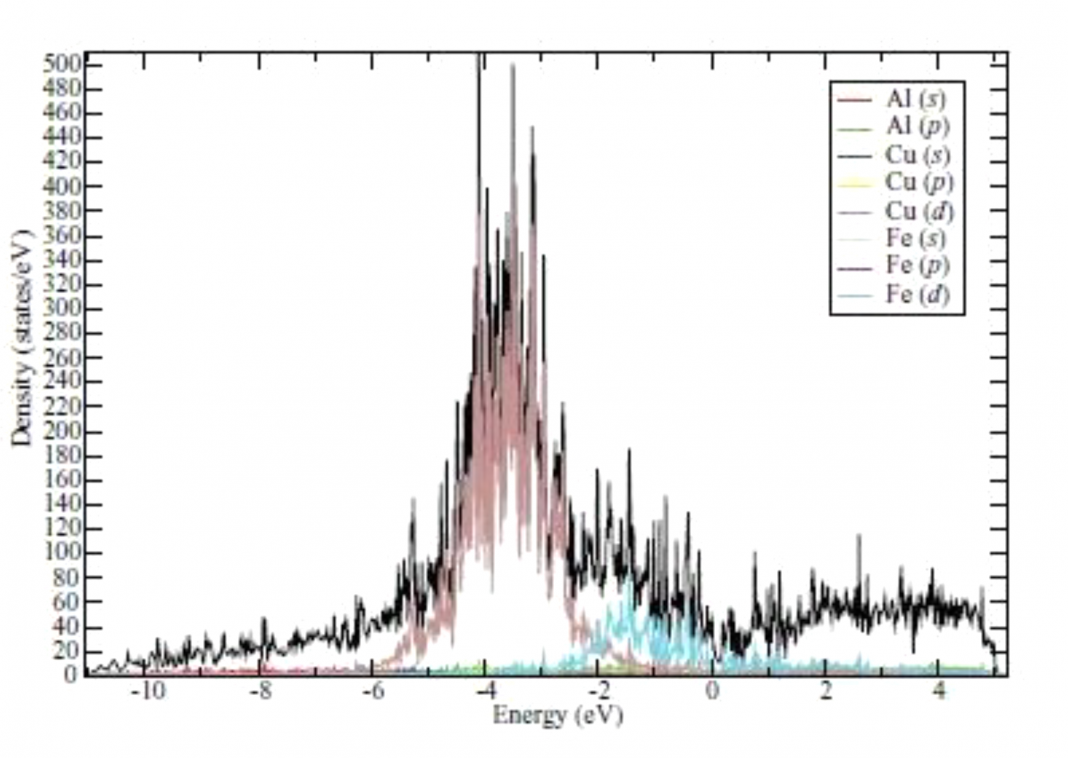
The spikiness of the density of states in quasicrystals

The spikiness of the electronic density of states in quasicrystals is believed to be inherent to QCs and so-called approximants (APs) to QCs

Solids have been traditionally divided into two categories: crystalline and amorphous. The dramatic discovery of an icosahedral Al-Mn alloy by Shechtman et al. ⁽¹⁾ in 1984 (Shechtman was awarded the 2011 Nobel Prize in Chemistry) extended this dichotomous division by introducing the notion of quasicrystals (QCs). These compounds possess a new type of long-range translational order, quasiperiodicity, and a non-crystallographic orientational order associated with the classically forbidden fivefold, eightfold, tenfold, and twelvefold symmetry axes ⁽²⁾. Whereas there are more than 20 million/tens of thousands known crystalline/amorphous compounds, QCs have hitherto been found in more than a hundred binary and ternary intermetallic systems ⁽³⁾. One of the central problems in condensed matter physics is determining whether quasiperiodicity leads to physical properties that are significantly different from those of crystalline and amorphous materials.

Spikiness of the electronic density of states in quasicrystals inherent to QCs and so-called approximants (APs) to QCs

The spikiness of the electronic density of states in quasicrystals is believed to be inherent to QCs and so-called approximants (APs) to QCs. The latter are structurally complex crystalline compounds in which the arrangements of atoms within their large unit cells closely approximate the local atomic structures in QCs ⁽⁴⁾. The first prediction of the spiky DOS structure in QCs and their APs was made in 1989 ⁽⁵⁾. Since then, numerous first-principles electronic structure calculations have predicted that the DOS consists of many fine spiked peaks with widths in the range of 10-50 meV (see figure below). One dissenting theoretical work ⁽⁷⁾ argues that the DOS spikiness is an artifact of calculations.

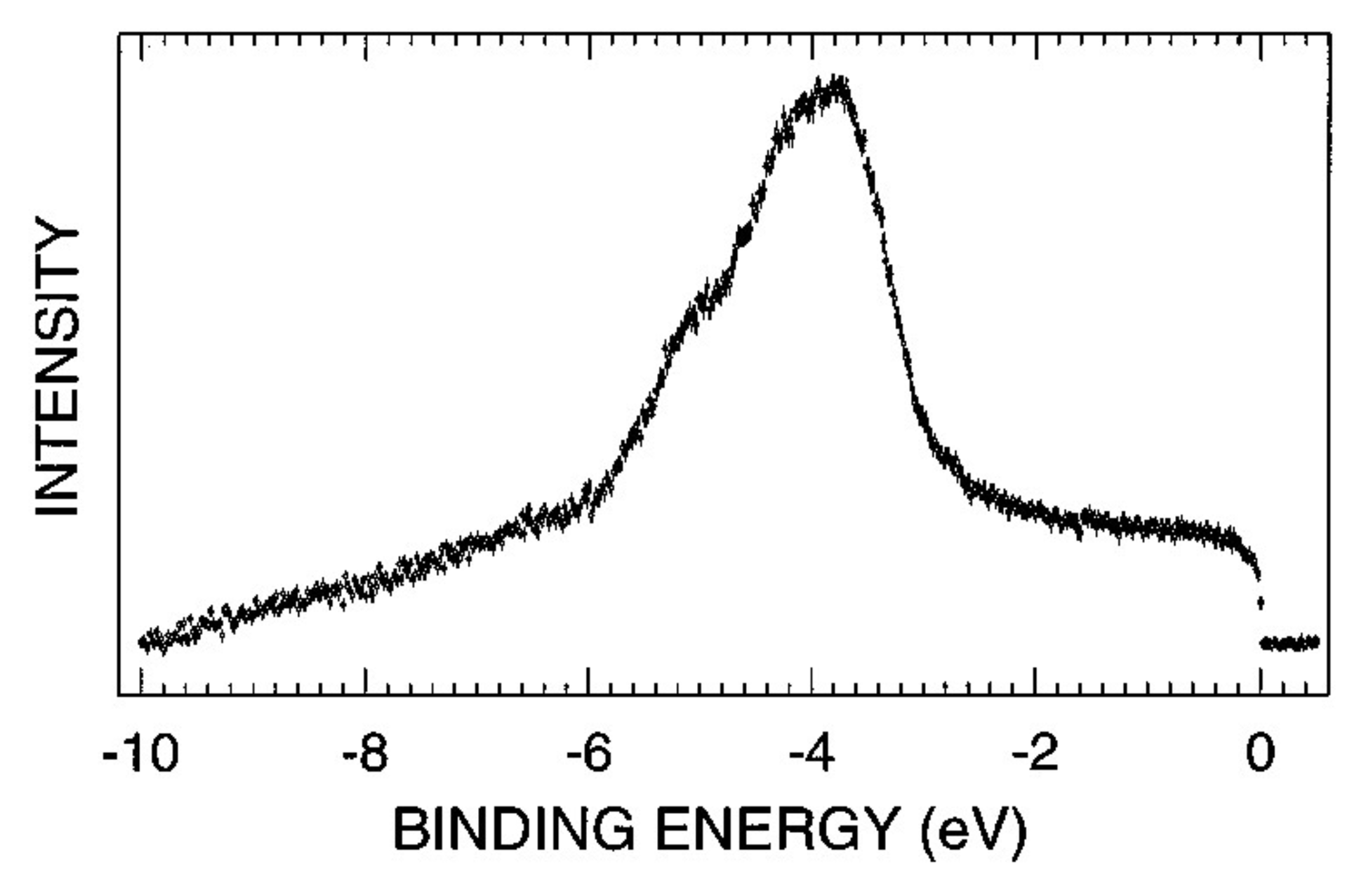
What is the controversy surrounding the spikiness of the electronic density of states in quasicrystals?

On the experimental side, there still is some controversy on the reality of the DOS spikiness. Ultrahigh-energy- resolution photoemission spectra of poly-grain ^(9-11) and single-grain ⁽⁸⁾ QCs failed to detect the presence of the expected DOS spikiness (see figure below). The first experimental indication for DOS spikiness was probably made based on the tunnelling spectra of the single-grain decagonal Al₇₃Ni₁₇Co₁₀ QC, which were “reminiscent” of the DOS spiky structure ⁽¹²⁾. The first definitive statement about the experimental signatures of the spiky DOS near the Fermi energy in the icosahedral Al₇₀Pd₂₁Mn⁹ QC was made in 2009 ⁽¹³⁾. Through a complex analysis of the scanning tunnelling microscopy spectra and the scanning tunnelling spectroscopy measurements, Widmer et al. ⁽¹³⁾ concluded that DOS spikiness occurs only on the nanometer scale and only in local DOS. It would appear that more high-energy and high-spatial resolution measurements for other high-quality QCs are required to convincingly state that the DOS spikiness is an inherent characteristic of QCs and their corresponding APs.

References

1. D. Shechtman, I. Blech, D. Gratias, and J.W. Cahn, Phys. Rev. Lett. 53, 1951 (1984).
2. Physical Properties of Quasicrystals, edited by Z.M. Stadnik (Springer-Verlag, Berlin, 1999).
3. W. Steurer, Z. Kristallogr. 219, 391 (2004); W. Steurer and S. Deloudi, Acta Crystallogr. A 64, 1 (2008).
4. A.I. Goldman and K.F. Kelton, Rev. Mod. Phys. 65, 213 (1993).
5. T. Fujiwara, Phys. Rev. B40, 942 (1989).
6.  D.Y. Young and W. Steurer, Phys. Rev. B84, 054116 (2011).
7. E.S. Zijlstra and T. Janssen, Europhys. Lett. 52, 578 (2000).
8. Z.M. Stadnik, D. Purdie, Y. Baer, and T.A. Lograsso, Phys. Rev. B64, 214202 (2001).
9. Z.M. Stadnik, D. Purdie, M. Garnier, Y. Baer, A.-P. Tsai, A. Inoue, K. Edagawa, and S. Takeuchi, Phys. Rev. Lett. 77, 1777 (1996).
10. Z.M. Stadnik, D. Purdie, M. Garnier, Y. Baer, A.-P. Tsai, A. Inoue, K. Edagawa, S. Takeuchi, and K.H.J. Buschow, Phys. Rev. B55, 10938 (1997).
11. R. Tamura, Y. Murao, S. Takeuchi, T. Kiss, T. Yokoya, and S. Shin, Phys. Rev. B65, 224207 (2002).
12. L. Guohong, H. Haifeng, W. Yunping, L. Li, L. Shanlin,
    J. Xiunian, and Z. Dianlin, Phys. Rev. Lett. 82, 1229 (1999).
13. R. Widmer, P. Gröning, M. Feuerbacher, and O. Gröning, Phys. Rev. B79, 104202 (2009).

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.