John H. Miller, Jr., from the University of Houston, Dept. of Physics and Texas Center for Superconductivity, walks us through superconductivity and related macroscopic quantum phenomena
Quantum behavior applies not only to microscopic but also to macroscopic systems. Spin-½ particles, fermions, obey the Pauli Exclusion Principle, whereby no two can occupy the same quantum state. By contrast, many integer-spin particles, bosons, can condense into a single macroscopic state.
In a superconductor (1), below its critical temperature or Tc , electrons condense into an electronic superfluid that flows with no resistance. For electrons (spin- ½) to condense, they must form pairs. There is one problem, however. Electrons normally repel each other.
Two issues were resolved in the Bardeen-Cooper-Schrieffer (BCS) theory of superconductivity. One is that the interaction of electrons with crystalline lattice vibrations (phonons) can cause a net attraction. Another is that pairing takes place in momentum space. Partners of each Cooper pair form a correlated wavefunction encompassing many other electrons in real space. The BCS theory, with phonon-mediated pairing and s-wave pairing symmetry, explained classic, low-Tc superconductors.
Things changed with the discovery of high-Tc superconductivity in cuprates, such as YBa2Cu3O7 (YBCO). Unlike classic superconductors, YBCO shows d-wave pairing symmetry, indicating non-phonon-based pairing. (The author’s group performed some key experiments at the University of Houston). Another aspect is that very high critical magnetic fields will enable powerful electromagnets for compact Tokamak fusion reactors.
Superconducting quantum computers
Quantum computing is one of the most recent applications of superconductivity. Most superconducting quantum computers use aluminum, with a Tc of 1.2 K. They rely on Josephson tunneling of paired electrons through a thin insulating barrier. The Josephson coupling energy causes a nonlinear kinetic inductance. This underlies the transmon qubit, essentially a nonlinear inductor-capacitor (LC) resonator. When cooled to milli-Kelvin (mK) temperatures, the transmon acts like an “artificial atom.” Two of its energy levels are designated as |0 and |1 states of the qubit.
Existing superconducting quantum computers, unfortunately, require mK cooling with dilution refrigerators. This limits their applicability due to large size, high cost, scarcity of 3He, and limited cooling power.
Quantum materials and systems
There is thus a need to reveal quantum materials and systems that can act as more thermally robust quantum resources.
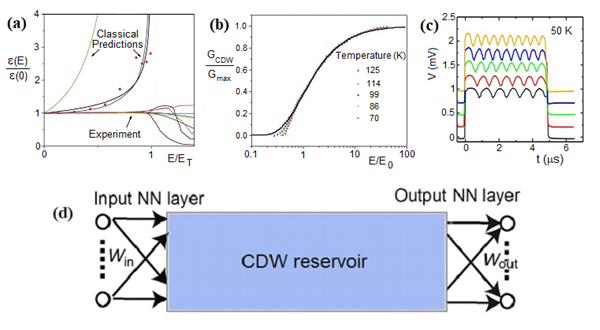
The charge density wave (CDW) is an electron-phonon condensate that forms in layered materials. (1,2) CDWs show collective electron transport at the highest known temperatures at ambient pressure, above the boiling point of water in some materials. Its quantum nature is revealed by experiments that include oscillations, of period h/2e, in CDW current vs. magnetic flux in TaS3 rings.
Some CDWs show evidence for quantum-enhanced learning. In the pulse-duration memory effect (PDME), one applies a series of rectangular current pulses, while the CDW responds with many voltage oscillations. After training, the final CDW voltage oscillation always finishes at a minimum, as if it knew the pulse length beforehand. 1-3 training pulses are needed, vs. hundreds to thousands, sometimes no learning, in classical simulations.
CDWs might thus be suited for quantum reservoir computing. A reservoir is a dynamical system, with neural network (NN) layers at its input and output, which reduces learning cost. Quantum reservoir computing and machine learning could emerge as pervasive technologies due to their broad applicability.
Other potential applications
Other potential applications include hybrid CDW-superconductor qubits for circuit-based quantum computing. In some proposed devices (3), the roles of which element is nonlinear are interchanged (vs. the transmon) in nonlinear LC and related resonators. Further advances will require revealing the underlying microscopic behaviors of CDWs and related macroscopic quantum systems.
References
- Bardeen, J. Superconductivity and Other Macroscopic Quantum Phenomena. Physics Today 43, 25-31, doi:10.1063/1.881218 (1990).
- Miller, J. H., Jr. & Suárez-Villagrán, M. Y. Quantum fluidic charge density wave transport. Applied Physics Letters 118, 184002, doi:10.1063/5.0048834 (2021).
- Miller, J. H., Villagrán, M. Y. S., Sanderson, J. O. & Wosik, J. Hybrid Quantum Systems for Higher Temperature Quantum Information Processing. IEEE Transactions on Applied Superconductivity 33, 1-4, doi:10.1109/TASC.2023.3241131 (2023).

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.


