Chris Jeynes ponders the reality of the Arrow of Time (the Second Law of Thermodynamics) and how it conditions the basic laws of physics
The thing is, we live first and die after. This inescapable fact has not stopped physicists from toying with the idea that, actually, Time’s Arrow is illusory. You see, it is also perfectly obvious to everyone that it’s the Sun that goes round the Earth – that’s simple common sense, but just because it’s “obvious” doesn’t make it “true” (everyone now knows that the Earth goes round the Sun)!
The Loschmidt Paradox
Physicists have now firmly established two fundamental Grand Theories: Quantum Mechanics (QM), the physics of the atomic, and General Relativity (GR), the physics of the cosmic. There is no doubt in anyone’s mind that these theories are broadly correct. The trouble is, all the Laws of both QM and GR are time-reversible: that is, they would look the same if time travelled backwards – the Laws appear to ignore the Second Law, and so it seems that the Arrow of Time is not basic! However, obtaining the observed thermodynamic behaviour (living first and dying after, not the other way round) using just the “fundamental” laws of QM and/or GR is fraught with difficulty: this is known as the Loschmidt Paradox.
The Second Law & quantum gravity
Another big problem for physicists is that although QM and GR are both excellent theories, they are also mutually incompatible (assuring us that something needs changing). So, the hunt is now on for a Theory of Quantum Gravity able to successfully unify the physics of the small with the physics of the large. But what if the Arrow of Time is indeed more fundamental than either (or both) of QM or GR?
Quantitative Geometrical Thermodynamics (QGT)
We have established a new approach to the thermodynamics of stability by showing that the geometry of any entity builds in the effect of the Second Law of Thermodynamics. So the DNA molecule is right-handed because of the Arrow of Time: this was proved by Michael Parker in 2010 and more rigorously in Appendix A of our 2019 paper. Buckminsterfullerene is stable because it takes a Maximum Entropy shape (proved in 2020). Similarly, the Maximum Entropy geometry of spiral galaxies (also proved in 2019) accounts for their ubiquity in the Universe. Of course, these things are already known, but the thermodynamics proofs are analytical and depend on no other physics: There’s something fundamental about QGT.
Thermodynamics of the Very Big
The celebrated Bekenstein-Hawking Equation (BHE) specifies the entropy of a black hole (BH). It remains the only widely accepted physics formula that explicitly includes QM and GR constants. It is now believed that all spiral galaxies have a central supermassive BH (SMBH), and the 2019 QGT demonstration of their stability was explicitly for a heavily idealised ‘galaxy’ consisting only of the central SMBH.
But in May 2021, we demonstrated independently (from QGT) that the BHE was only a particular case of a more general holographic relation that also applied to nuclear entities. So, now the BHE has three independent derivations: originally from statistical mechanics, then from string theory, and now from QGT. In August 2021, we calculated the entropy production of BHs and demonstrated the strange and very far-reaching result that, like energy, entropy production (implying dissipation) is a conserved quantity. For physicists, the idea that dissipative processes can be conservative is weird.
Thermodynamics of the Very Small
The alpha particle (4He) is also extraordinarily stable. Using our generalisation of the BHE, we demonstrated (in February 2022) that when we treat the alpha as a unitary entity (than which there exists nothing simpler), we can correctly calculate its size purely from QGT and using no QM at all. Moreover, we also correctly calculate the nuclear sizes not only ofthe helium isotopes (6He,8He – see Figure) but also of the “helium series” (4He,8Be,12C,16O, 20Ne,24Mg,28Si,32S,36Ar,40Ca: these results appear not to be available from QM).
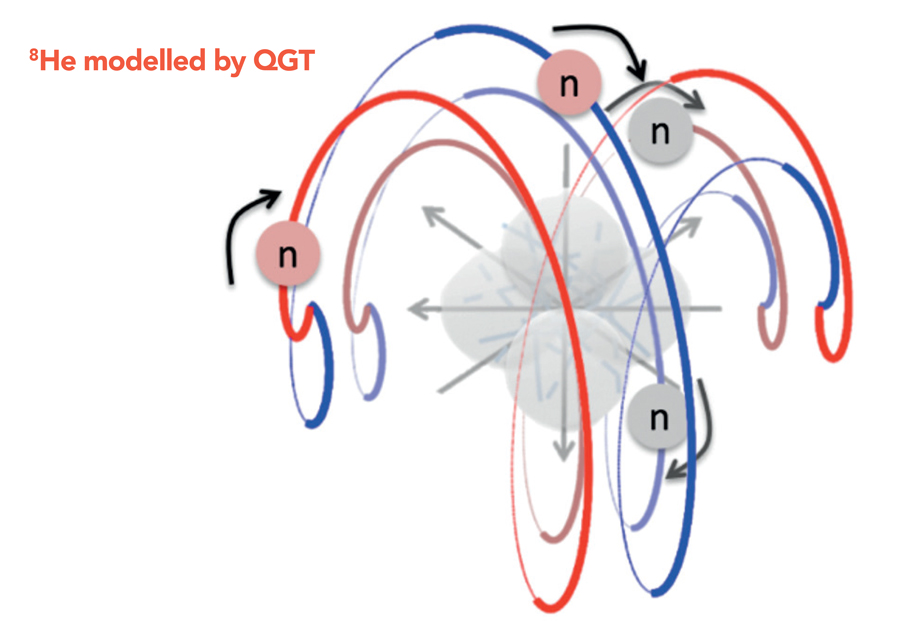
The 8He nucleus is modelled in QGT as an alpha particle with a four-neutron shell which is a holomorphic pair of holomorphic neutron pairs. See Parker et al. (2022), for image see the journal Table of Contents. The 8He nucleus has an observed matter radius of 2.49±0.04 fm and a matter radius calculated by QGT as 2.51 fm
Time is Complex
The mathematical apparatus of QGT is rather heavy and very unfamiliar: unfortunately, physical simplicity always seems to have the price of mathematical impenetrability. We have now shown (November 2022) that time itself is most elegantly represented as a complex number. Such a formalism allows a “simple” and coherent treatment of both reversibility and irreversibility, directly addressing the Loschmidt Paradox.
This coherent treatment is more familiar than expected. When light travels through a medium, there is a “dispersion relation” (examples are the rainbow or the spectrum out of the prism), and there may be absorption of the light. The physicists handle all this through the “refractive index”, a complex number where the “imaginary” component accounts for light absorption.
It turns out that the “dispersion relation” is entirely general, and one can treat the system energy and the system entropy production as two sides of the same coin. This is another very far-reaching result that is also strange since although we are used to regarding energy as the vital quantity of physics, dissipation has always been treated as an annoying imperfection of the system. However, we know that everything interesting in the world involves irreversibility (and dissipative processes), so it’s rather comforting that these things can now be formally understood in the same way we treat energy.
Theory of Everything
We have demonstrated that QGT can handle quantum and cosmic scales equally well: the Second Law of Thermodynamics is treated as basic (not as “emergent” from QM). We have shown that QGT handles irreversible systems seamlessly with the reversible ones that physicists have mostly been interested in, showing how an entirely general treatment is both mathematically elegant and also tractable.
It is disconcerting that what looks like a Theory of Everything emerges unexpectedly from a most unlikely quarter: thermodynamics has been considered the province of the chemists even though physicists have made significant breakthroughs (Chemistry Nobel Prizes to Onsager in 1968 for his ‘reciprocal relations’ and to Prigogine in 1977 for his ‘theory of dissipative structures’).
But our intuition on the reality of Time’s Arrow (living first and dying after) appears correct in this case: the Second Law really is fundamental.