Thermodynamics of hadronization: The rotating lepton model explains key CERN experiments

Constantinos G. Vayenas, Professor at the University of Patras, Academy of Athens, explores the thermodynamics of hadronization, using the Rotating Lepton Model and two key CERN experiments

The observation of neutrino production in the recent pp collision CERN experiments ⁽¹⁾ has confirmed that hadrons consist of neutrinos. ⁽²⁾ This is also confirmed by the observed hadron and boson formation during the e+-e- annihilation experiments at CERN ⁽³⁾, where positrons and electrons have been shown to catalyze hadron formation from ambient neutrinos. ⁽⁴⁾

The Rotating Lepton Model (RLM) of composite particles ⁽⁵⁾, along with classical thermodynamics, describe the reaction 3ν₃ ⇌ n of the formation of a neutron from three ultrarelativistic heavy neutrinos of rest mass m₃=0.0437 eV/c2 each. The RLM provides a semiquantitative fit to the chemical potential (or Gibbs free energy) vs T data of Stachel et al. presented in [6] and [7]. This suggests that the reaction 3ν₃ ⇌ n plays a dominant role in hadron formation and decomposition.

Hadronization is the process of formation of hadrons out of their constituents, which are currently known as quarks and gluons. This process apparently first occurred on a very large scale shortly after the Big Bang when the quark-gluon plasma cooled to the temperature where free quarks and gluons cannot exist, estimated by quantum chromodynamics (QCD) to be in the 150 to 220 MeV range. The quarks and gluons then combined into hadrons.

Hadronization on a very short scale can be studied currently after high energy collisions in particle colliders in which quarks and gluons are created, but due to colour confinement cannot exist individually. ⁽⁶⁾ According to the Standard Model (SM) they combine spontaneously with quarks and antiquarks created from the vacuum to form hadrons. The Quantum Chromodynamics (QCD) of the hadronization process are not yet fully understood but are modelled in a number of studies ^(6-9) which also examine the thermodynamics of the quark-gluon condensation. ^(4,5)

Interestingly, the main experimental process for hadronization in particle colliders is e⁺e^– annihilation at √s ≈ 10 to 200 GeV. ^(6,9) No quarks are directly observed but, remarkably, it is found that the e⁺e^– annihilation event can cause pronounced hadronization i.e., up to at least 20, hadron multiplicities. Specifically, a single e⁺c^– pair can produce 21.2 π⁺ mesons, up to 3 K⁺ kaons, but only up to 1.41 protons and 0.4 ʌ particles. ⁽⁹⁾

Another powerful technique leading to the formation of hadrons is the high-energy collisions between heavy nuclei, leading to the intermediate formation of a deconfined state of matter that exists at phenomenally high temperatures and pressures. This “quark-gluon plasma” is thought to have permeated the first microseconds of our Universe before it condensed to form hadrons and other composite particles. During the last 20 years, the creation and, most importantly, the condensation of the quark-gluon plasma has been the focal point of a plethora of experimental and theoretical investigations. ^(6-9)

It is worth examining the thermodynamics of this extremely important process from the point of view of the RLM ^(2,4,10-15) of hadronization which is based on the pronounced relativistic increase in mass with particle speed ^(2,16) and, surprisingly, one notes a very close connection between quark-gluon plasma condensation and the RLM of hadronization.

Key features of the Quark-gluon plasma condensation

One of the key points of the Quark-gluon condensation or its reverse process known as “the onset of deconfinement” is the establishment of equilibrium between hadrons and the quark-gluon plasma. The latter refers to the deconfinement of the hadronic phase with the simultaneous production of deconfined quarks and gluons in the so-called fireball, which can then recombine to form hadrons.

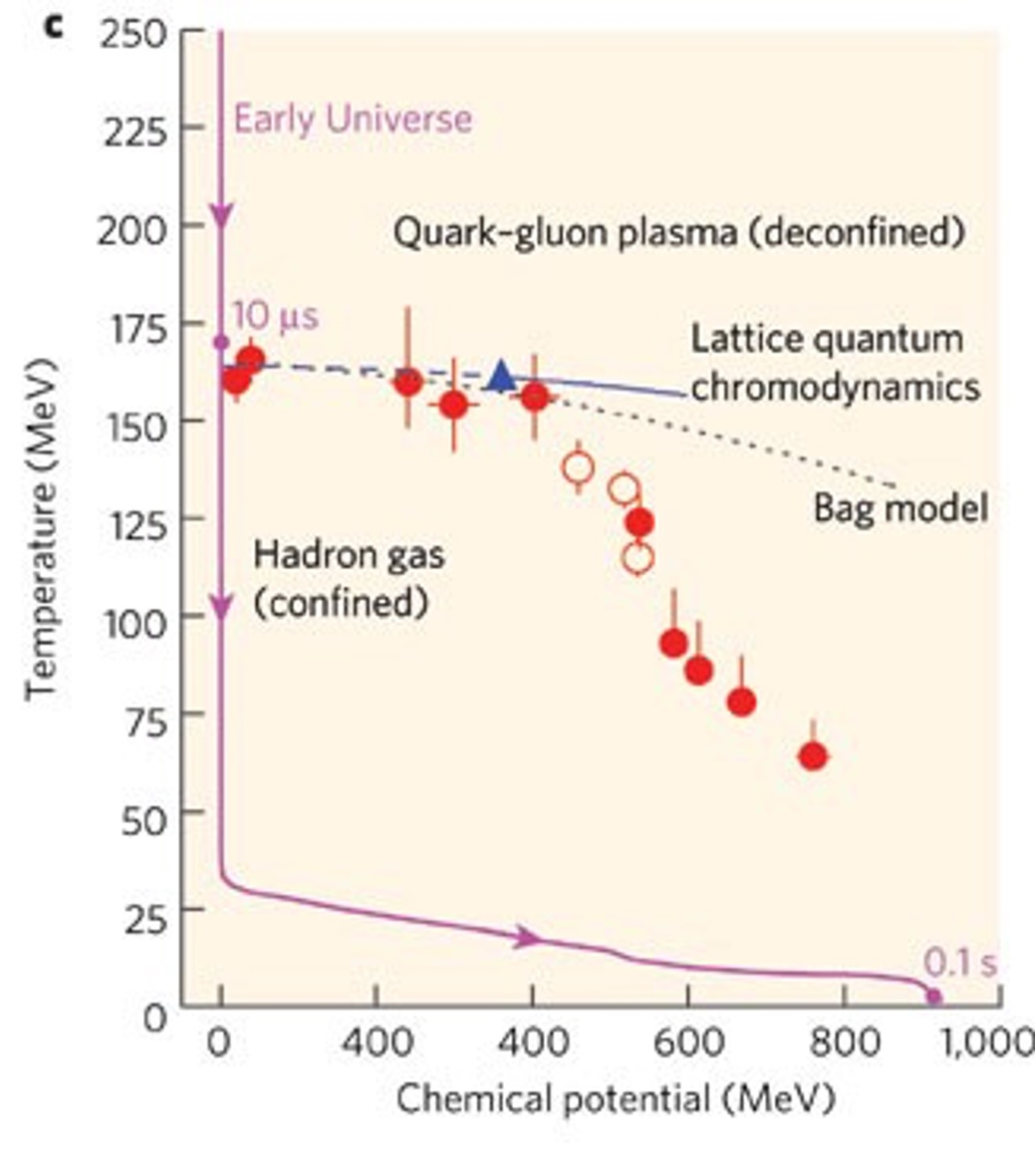
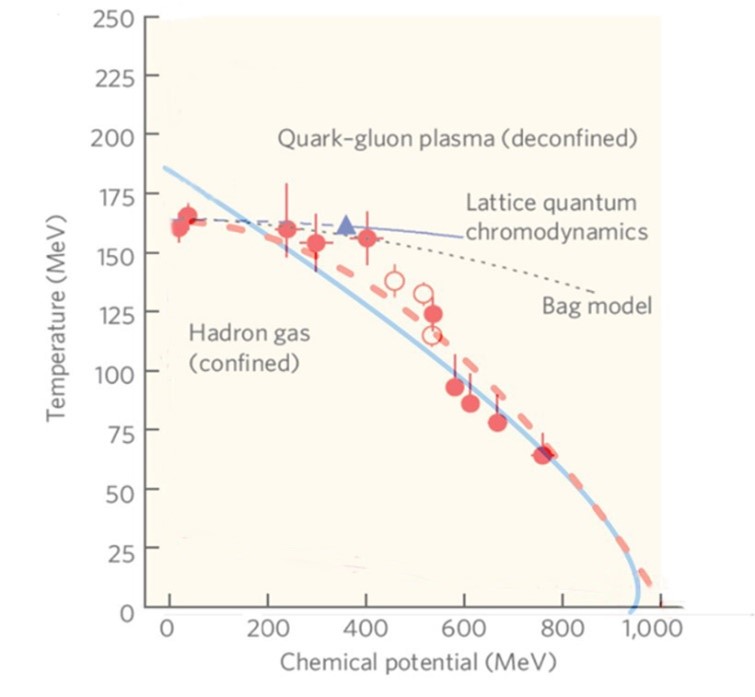
Various simple estimates lead to a critical temperature of the order of k_bT=100 MeV for the transition between the quark-gluon plasma and the familiar confined hadronic phase of matter. In an important paper in 1963, R. Hagedorn discovered a limiting temperature for hadronic systems around the π-meson mass of 140 MeV/ c². This temperature of k_bT=140 MeV is considered the critical temperature for the deconfinement phase transition. The thermodynamics of the “fireball” are summarised in Figure 1.

These data have been described successfully by Gazdzicki, Gorenstein and Seyboth ⁽⁷⁾ for the cases of Pb-Pb and Au-Au nuclei collisions by the following simple expression:

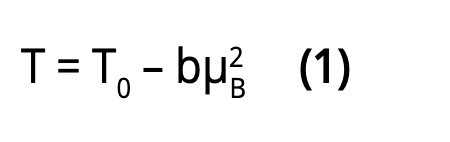
with T₀=165 MeV and b=0.1583 GeV^-1.

Key features of the Rotating Lepton Model of hadronization

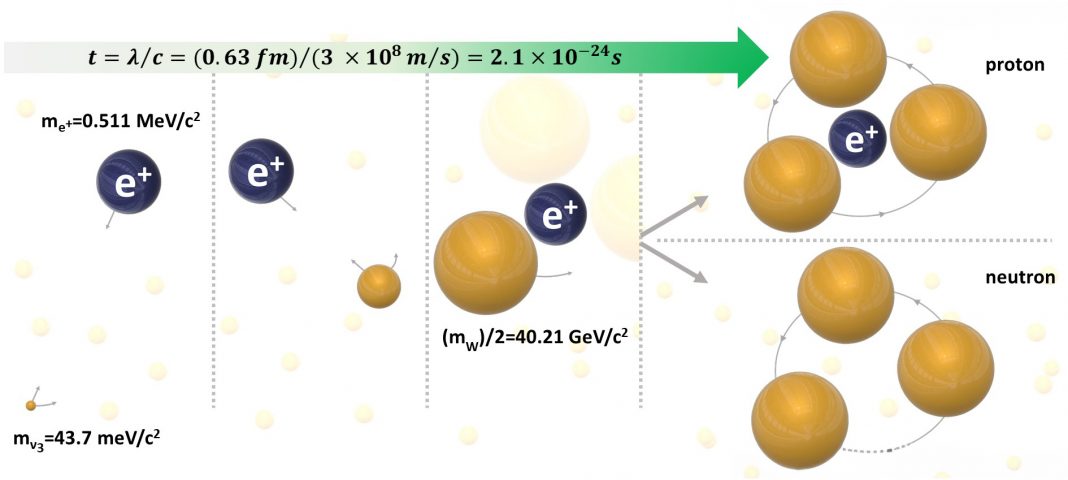
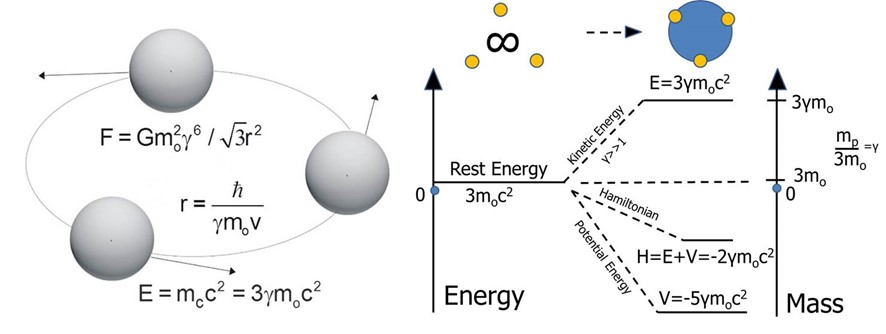
According to the RLM, protons and neutrons are formed by three neutrinos caught in circular orbit as a result of their strong gravitational attraction, which, due to their relativistic velocities, increases their mass and transforms them into quarks (Fig. 2). The proton is assumed to have a positron at the centre of rotation. ^(10,13,15)

Thermodynamics of the RLM

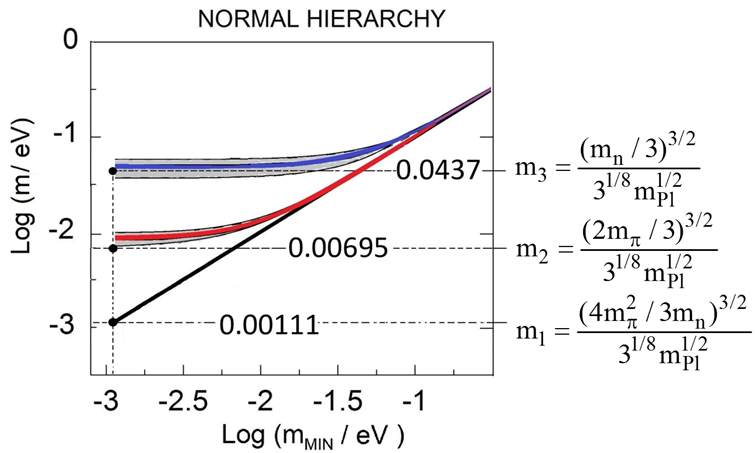
When the three rotating neutrinos are of the ν₃ type of the normal hierarchy (highest mass neutrino) (Fig. 3), then a neutron is formed:

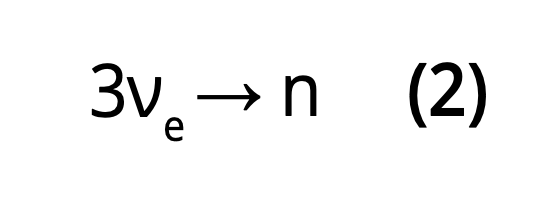
The thermodynamics of this process are interesting:

As shown in Figure 2, the enthalpy change at T=T_o (defined from ΔG^o=0) is given by [2,15]

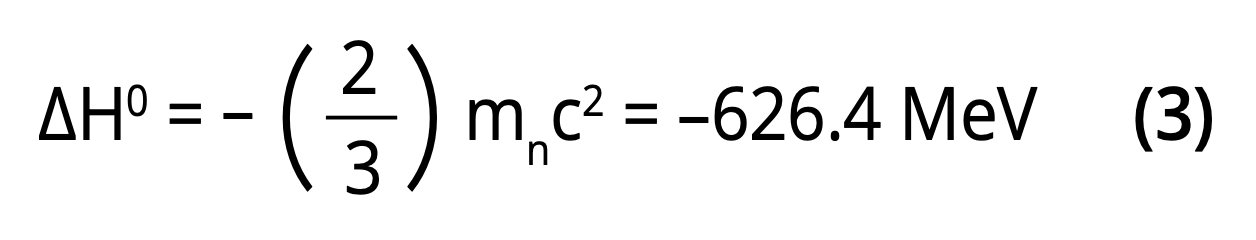
and the corresponding entropy change for an ideal gas is to a first approximation:

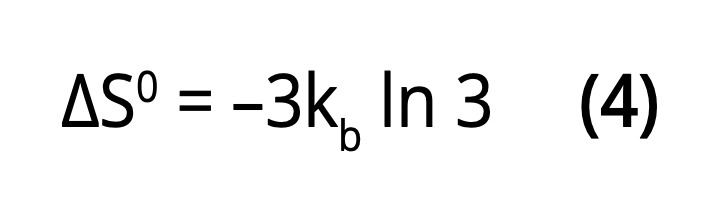
Consequently, the Gibbs free energy (chemical potential)

can be used to define the reference temperature T_o, i.e., ΔG^o=0, via

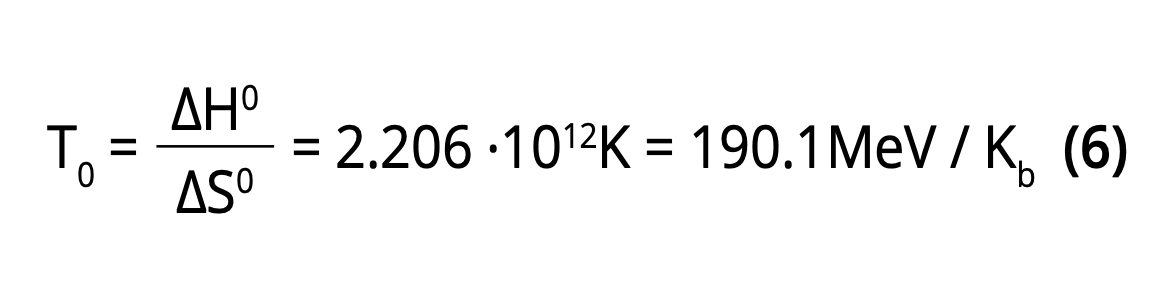
With a combination of equations (3-6) one obtains.

A plot of equation (7) is given in Figure 4 and compared with the classical Quark-Gluon plasma condensation Figure 1. ⁽⁶⁾ The agreement is striking.

This curve fits very well with the experimental data on the phase diagram for strongly interacting matter ⁽⁶⁾, as shown in Figure 4.

Given Figure 4, it becomes clear that all the key features of the quark-gluon plasma condensation can be described via the RLM.

It is worth noting that the slope of the deconfinement line in the T-μ (or T-G) diagrams is near 5.2 kb and provides a direct indication of the number of particles (three) involved in the hadronization process 3ν_e → n, via.

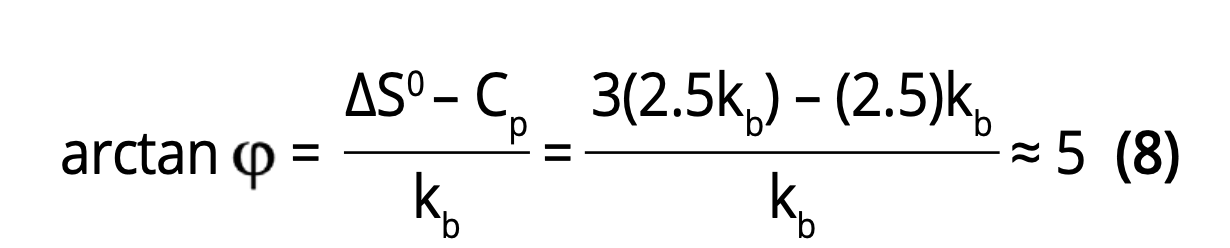
This implies that based on these diagrams one may conclude that three neutrinos (or quarks, which have the same rest mass as neutrinos [2,15]) are involved in the hadronization– dehadronization process controlling the quark gluon plasma confinement and deconfinement.

References

1. Henso Abreu et al., First Direct Observation of Collider Neutrinos with FASER at the LHC, Physical Review Letters(2023).
2. C.G. Vayenas, S. Souentie, Gravity, special relativity and the strong force: A Bohr-Einstein-de Broglie model for the formation of hadrons. Springer, New York, (2012).
3. R.L. Workman et al. (Particle Data Group) (2022) The review of particle physics. Prog. Theor. Exp. Phys 2022:083C01.
4. C.G. Vayenas and D.G. Tsousis, “The catalytic role of Electrons and Positrons in the synthesis of Chemicals and of Hadrons”, Topics in Catalysis 66, 1280–1284 (2023).
5. C.G. Vayenas, S. Souentie, & A. Fokas, A Bohr-type model of a composite particle using gravity as the attractive force. Physica A, 405, 360 (2014).
6. P. Braun-Munzinger and J. Stachel, The quest for the quark–gluon plasma. Nature, 448, 302–309 (2007).
7. M. Gazdzicki, M. Gorenstein, P. Seyboth, Onset of Deconfinement in Nucleus–Nucleus Collisions: Review for Pedestrians and Experts. Acta Phys. Pol. B 42, 307 (2011).
8. M. Gaździcki and M.I. Gorenstein, On the early stage of nucleus-nucleus collisions. Acta Physica Polonica B, 30, 2705-2735 (1999).
9. F. Becattini, J. Manninen, M. Gazdzicki, Energy and system size dependence of chemical freeze-out in relativistic nuclear collisions. Physical Review C, 73, 044905 (2006).
10. C.G.Vayenas, A.S. Fokas, D. Grigoriou, On the structure, masses and thermodynamics of the W+ bosons. Physica A, 450, 37-48 (2016).
11. A.S. Fokas, C.G. Vayenas, On the structure, mass and thermodynamics of the Zo bosons. Physica A, 464, 231-240 (2016).
12. A.S. Fokas, C.G. Vayenas, D.P. Grigoriou, On the mass and thermodynamics of the Higgs boson. Physica A, 492, 737 (2018).
13. C.G. Vayenas, D.P. Grigoriou. Hadronization via gravitational confinement, in A. Studenikin (Ed.), Proc. of the 18th Lomonosov conference, in Particle Physics at the Year of 25th Anniversary of the Lomonosov Conferences. World Scientific, 2019. pp. 517-524.
14. C.G. Vayenas, D. Grigoriou, and E. Martino, Proton internal pressure distribution suggests a simple proton structure. J. Mech. Behavior of Materials, 28, 1-9 (2019).
15. C.G. Vayenas, D. Tsousis, and D. Grigoriou. Computation of the masses, energies and internal pressures of hadrons, mesons and bosons via the Rotating Lepton Model. Physica A, 545, 123679 (2020).
16. A.Einstein,ZürElektrodynamikbewegterKörper. Ann. Phys. 17, 891 (1905); English translation on the electrodynamics of moving bodies, G.B. Jeffery, W. Perrett (1923).
17. R.N. Mohapatra et al (2007) Theory of neutrinos: a white paper. Rep Prog Phys 70:1757-1867.
18. Takaaki Kajita, Discovery of neutrino oscillations. Rep. Prog. Phys. 69, 1607 (2006).

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.