Why gravitational waves cannot exist!

J-F Pommaret from CERMICS, Ecole des Ponts ParisTech, France, investigates the idea that gravitational waves cannot exist

1) A very long search:

In 1969, I decided to become a visiting student of D. C. Spencer at Princeton University and to apply these new tools in General Relativity (GR). A book published in 1978 from my PhD thesis and translated into Russian, started my research work. By analogy with Maxwell’s equations for electromagnetism (EM), to deciding about the existence of a potential for Einstein equations in a vacuum has been proposed in the meantime as a $1,000 challenge by J. Wheeler, a friend of Spencer.

No progress was made during the next 25 years, until I gave a negative answer in 1995, contrary to what the GR community believed. Wheeler sent me back a letter with a one-dollar bill attached, refusing to admit this result. Indeed, while teaching elasticity, I proposed an exercise explaining why a dam made with concrete is always vertical on the water-side with a slope of about 42 degrees on the other free side in order to obtain a minimum cost and the auto-stability under cracking of the surface under water (See the Introduction of [2] and Zbl 1079.93001). The main tool was the approximate computation of the Airy function inside the dam. I discovered that the Airy parametrization was just the adjoint of the (linearized) Riemann operator used to generate compatibility condition (CC) for the deformation tensor by any engineer. Being involved in GR with A. Lichnerowicz, I got the idea of using the adjoint of an operator in a systematic way.

Then I found the recently published Master’s thesis of the Japanese student M. Kashiwara. It has been a shock to discover this mixing up of differential geometry and homological algebra, culminating in the use of the Differential Extension Modules. In particular, if Dξ = η has the generating CC D₁η = 0, then ad(D) may not generate all the CC of ad(D₁) and ext¹(M) ”measures” this gap only depending on the differential module M defined by D [2, 3]. Hence, exactly like homological algebra brought a revolution in mathematics, it will bring a revolution in physics. I also noticed that GR could be considered as “a” way to parametrize the Cauchy = ad(Killing) operator, leading to Gravitational Waves (GW).

It follows that the same confusion has been done by E. Beltrami (1892) and A. Einstein (1915) because they both used the same Einstein operator, not knowing it was self-adjoint.

Accordingly and until now, the GR community has never wanted to take these new tools into account and [6] provides a good example of such a poor situation both with the reason for which no other reference can be given. By chance, the control community has been interested during a while by these new techniques for studying OD or PD control systems with constant coefficients, thanks to U. Oberst. Hence, the impossibility to parametrize Einstein equations in a vacuum can only be found in books on control theory [Springer LNCIS 256, 2000 and 311, 2005].

Studying the Lanczos problems in 2001, I discovered that the Beltrami = ad(Riemann) operator can be parametrized by the Lanczos = ad(Bianchi) operator in the adjoint sequence. As a byproduct, the purpose of this pamphlet is to explain without any computation, the previous confusion between the Cauchy = ad(Killing) operator and the Bianchi operator. According to H. Poincaré, the geometrical and physical long exact dual differential sequences of operators acting on tensors, giving order of operators and number of components, are:

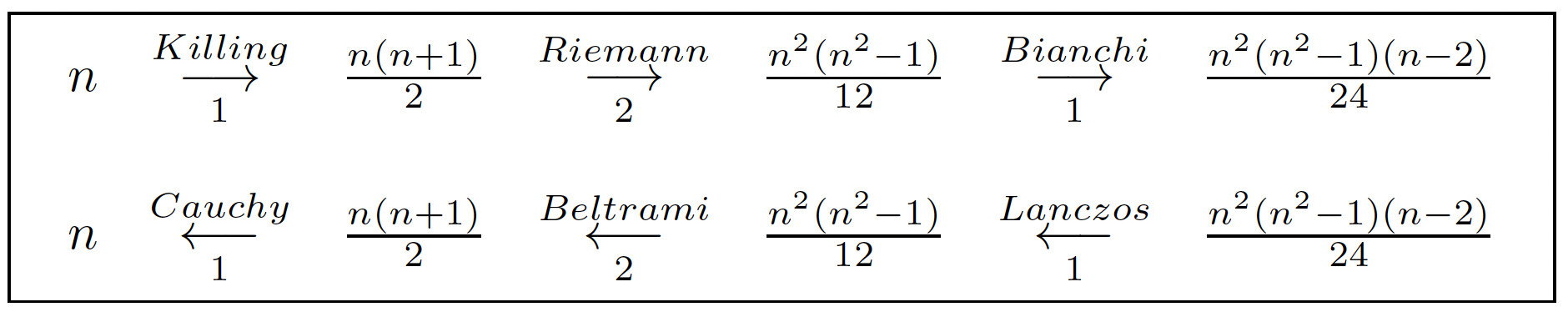
2) A basic control example:

Let a rigid bar be able to move horizontally with reference position x and attach two pendulums with lengths l₁ and l₂ making the (small) angles θ1 and θ2 with the vertical. The system for η = (x, θ¹, θ²) with gravity g is D₁η = 0:

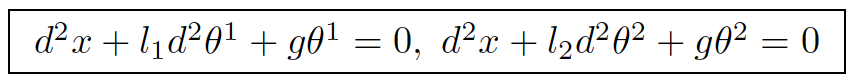
With a little skill, one can stop any movement by just moving the bar horizontally along itself iff l₁ ≠/ l₂. Equivalently, the system is controllable iff the operator ad(D₁) is injective, without using the Kalman test (1960) [3].

Multiplying the equations by λ¹ and λ², adding and integrating by parts, one gets ad(D₁)λ = 0, namely:

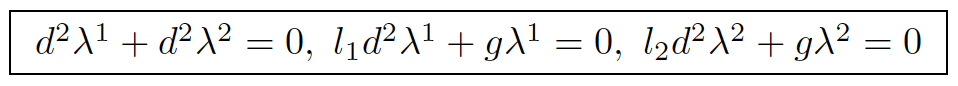
Differentiating twice, one may find iff l₁ ≠/ l₂:

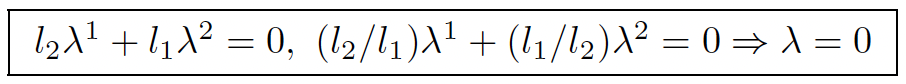
One finally obtains a fourth order (!) parametrization Dφ = η:

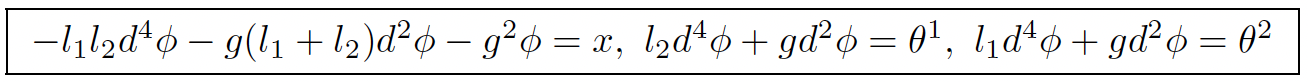
This parametrization is injective and we have the short exact dual sequences:

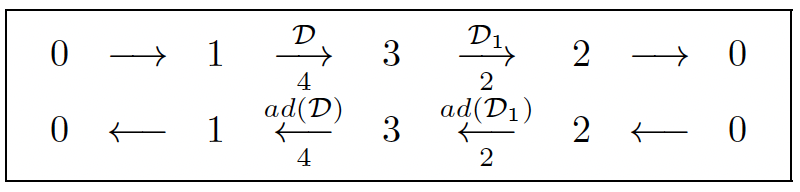
If l₁ =l₂ =l, then z = θ¹–θ² is satisfying the OD equation ld²z+ gz = 0. Contrary to what most engineers believe, I proved in 1995 [2, 3] that CONTROLLABILITY IS A STRUCTURAL PROPERTY OF A CONTROL SYSTEM THAT DOES NOT DEPEND ON THE CHOICE OF THE INPUTS AND OUTPUTS AMONG THE SYSTEM VARIABLES.

3) Differential double duality:

The following constructive test with 5 steps largely supersedes the Kalman test [2, 3, 7, 8]: Start with D₁, construct ad(D₁), then find its CC in the form of an operator ad(D). Finally, denoting by D₁′ the CC of ad(ad(D)) = D, the parametrization exists if, and only if we may have D₁’ = D₁. Indeed, as ad(D) ° D = 0, then D₁ is surely among the CC of D but other CC may also exist along the following diagram:

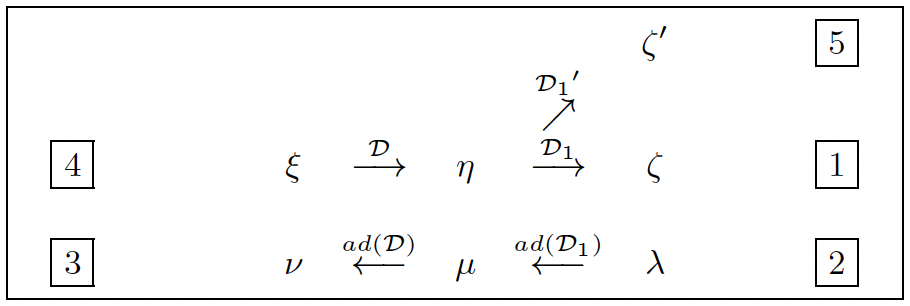
One can prove that each new CC brought by D′₁ that is not already a differential consequence of D₁ provides a quantity satisfying at least one OD or PD equation for itself.

4) Beltrami (1892) versus Einstein (1915):

Linearizing the Ricci tensor ρij over the Minkowski metric ω, we obtain the Ricci operator for the perturbation Ω of ω:

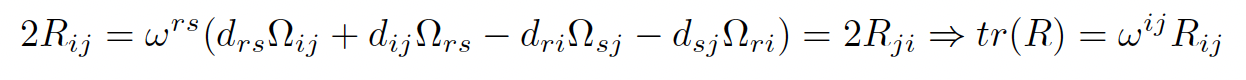
with 4 terms and the Einstein operator by setting Eij = Rij − (1/2)ωijtr(R) with 6 terms.

When n ≥ 3, the right part of the Killing resolution of the first section projects onto:

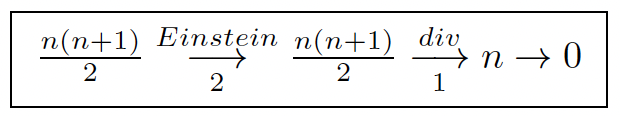
The Einstein operator is self-adjoint (a crucial property for which I don’t know any reference !!!), and we may get successively the five steps with ad(Einstein) = Einstein:

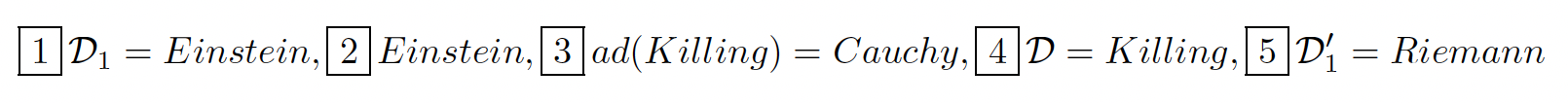
We obtain the strict symbolic inclusion D₁ ⊂ D’₁ in the diagram existing when n = 4:

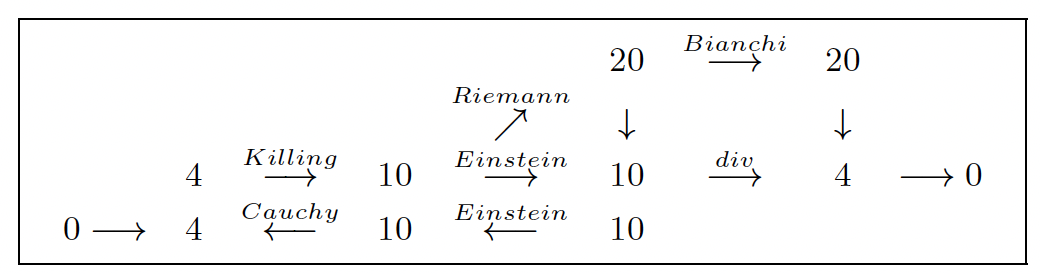
The Cauchy and Killing operators (left side) have thus strictly nothing to do with the Bianchi and therefore div operators (right side). In addition, the 10 stress potentials are no longer tensors but tensor densities and have nothing to do with the perturbation Ω of the metric. According to section 3, the 20 − 10 = 10 new CC are generated by the 10 independent components of the Weyl tensor, each one being killed by the D’Alembertian, a striking result totally unknown in this framework!!!

Already in 2017, I proved that GW cannot exist, not because of a problem of DETECTION but because their EQUATION is just the ad(Ricci) operator with the same previous comments.

When n = 2 in plane elasticity, one has (Compare to the double pendulum!):

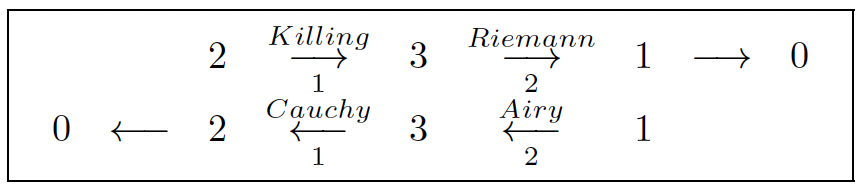
Multiplying the Riemann operator D₁ : Ω→d₂₂ Ω11 + d₁₁ Ω22 – 2d12 Ω12 by a test function φ and integrating by parts, we obtain the Airy = ad(Riemann) (Who knows !) parametrization σ11 = d₂₂ φ, σ¹² = σ²¹ = -d12 φ, σ²² + d₁₁φ of the Cauchy operator provided in 1863.

When n = 3, E. Beltrami introduced in 1892 the 6 stress functions φij = φji in the self-adjoint Beltrami = ad(Riemann) parametrization. The identification Lanczos = ad(Bianchi) leads to the long exact dual sequences, with the same confusion as Einstein but … 25 years before:

5) General relativity and gauge theory: Beyond the mirror!

Only the bottom row and the right column are known in the following commutative and exact algebraic Fundamental diagram II of tensors that I found in 1983 (1, p 446). A diagonal snake chase proves that Ricci ≃ S₂T* wheb g^₂ is the second order symbol of the infinitesimal Lie equations of the conformal group of space-time (8,9). This result explains the confusions done by A. Einstein and H. Weyl in their tentatices to use the lower sequence for linking GR and EM, through the splitting T* ⊗ T∗ ≃ S₂T∗ ⊕ ∧²T∗ ≃ (Rij) ⊕ (Fij) and the Spencer δ-cohomology:

Such a mathematical fact is in total contradiction with the use of the unitary group U(1) in Gauge Theory (GT) which is not acting on space-time. Paraphrasing W. Shakespeare, we may finally say:

“TO ACT OR NOT TO ACT, THAT IS THE QUESTION!”

References:

1. Partial Differential Equations and Group Theory, 1994, DOI: 10.1007/978-94-017-2539-2
2. Partial Differential Control Theory, Kluwer, 2001, ISBN: 978-94-010-3845-4
3. Algebraic Analysis of Control Systems Defined by PDE, 2005, ISBN: 978-1852339234. Springer, LNCIS 311, 2005
4. Spencer Operator and Applications, 2012, DOI: 10.5772/35607
5. How Many Structure Constants do Exist …, 2022, DOI: 10.1007/s11786-022-00546-3
6. Killing Operator for the Kerr Metric, 2023, DOI: 10.4236/jmp.2023.141003
7. Gravitational Waves and the Parameterization …, 2024, DOI: 10.5772/ intechopen.1000851
8. From Control Theory to Gravitational Waves, 2024, DOI: 10.4236/apm.2024.142004
9. Gravitational Waves and the Foundations of Riemannian Geometry, ISBN 979-8-89113-607-6