Quark generation via gravitational capture of neutrinos in circular orbits around positrons or electrons

We consider the circular motion of a neutrino of rest mass m_ν rotating around an electron or positron due to their gravitational attraction, and we use Special Relativity (SR) to compute the gravitational (or inertial) mass γ3mν of the neutrino. The computed mass is found to be, surprisingly, in the Planck mass range (~10¹⁹ GeV/c²), and the corresponding gravitational force between any two of them reaches the Strong Force value (10⁴-10⁵ N) at fm distances.

These results demonstrate the nature of quarks as relativistic neutrinos forming rotating equilateral triangles and constituting the basis of the Rotating Lepton Model (RLM) of hadrons and quarks, which is in very good agreement with the experimental mass values of hadrons and bosons.

For the last fifty years, quarks have been theorized by the Standard Model as basic constituents of hadrons. Their masses are of the order of 100 MeV/c2 to 100 GeV/c².

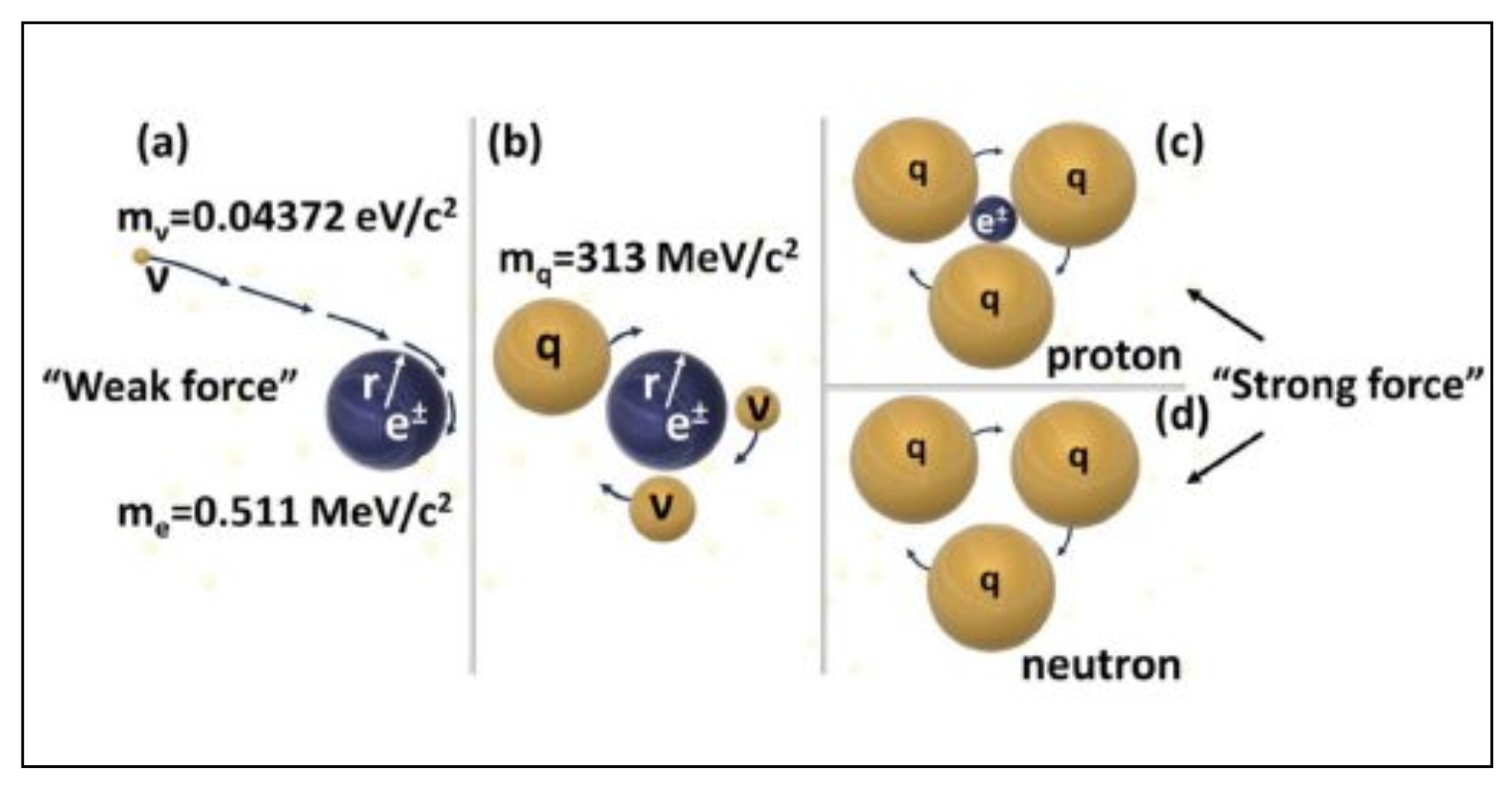
According to the Standard Model, quarks are considered to interact via gluon exchange [2]. However, close examination of literature particle tables has shown that the eventual decay products of all composite particles are only five, i.e., the positron e⁺, the electron e^–, and the three neutrinos of rest masses m₁, m₂, and m₃ (Figure 1) [3]. Due to the well-established principle of microscopic reversibility [4], the same five particles would be expected to be the building blocks of hadrons.

However, this is not the case according to the Standard Model (Fig. 2) due to the huge mass gap between leptons (neutrinos, e^±) and hadrons (baryons, mesons). Also, the so-called Strong Interaction, which maintains the stability of hadrons, is not theorized to act between leptons, such as neutrinos and electrons/positrons.

The recent development of the Rotating Lepton Model (RLM) bridges the mass gap between neutrinos and hadrons in a simple fashion (Fig. 2) and interprets the Strong and Weak Forces as relativistic gravity [5].

Gravity is, at a first glance, too weak to hold leptons together inside hadrons, due to their extremely small masses. However, special relativity [7,8] has been shown to play a dominant role in describing the Strong force as gravity between fast particles [5,9].

The Rotating Lepton Model (RLM) describes composite particles as triads of rotating superrelativistic neutrinos. Its structure and basic equations are shown in Fig. 3. If a positron (or electron) occupies the rotational center, then a proton (or antiproton) is formed. If the rotational center remains vacant, then a neutron is formed.

Recent work summarized here has shown that the relativistic speeds of neutrinos can be more easily achieved when an electron or positron interacts with neutrinos (Fig. 4). As a result, electrons and positrons have been found to act as catalysts for hadron production (hadronization) from neutrinos.

If we consider a rotating ring comprising one or more neutrinos together with one or more electrons/positrons, then the requirement for equal angular momenta of all rotating particles leads to γ_νm_ν=γ_em_e, thus the ratio

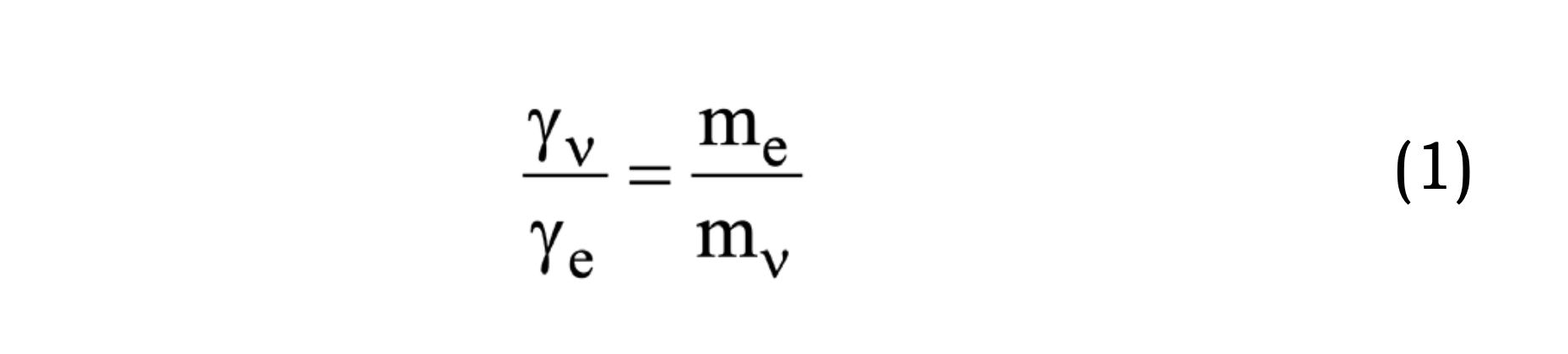
becomes enormous, i.e. equal to

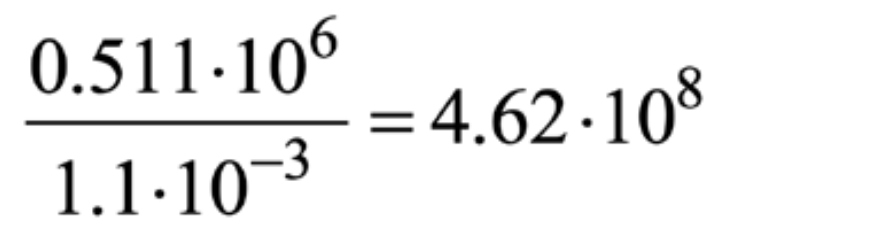
for ν¹ neutrinos, 7.35•10⁷ for ν₂ neutrinos and 1.17•10⁷ for ν³ neutrinos. If we consider such a rotating e — ν ring as a possible

candidate for the W^± boson structure, then its relativistic mass should equal the observed experimental boson mass, i.e. γ_em_e=80.42 GeV/c² thus,

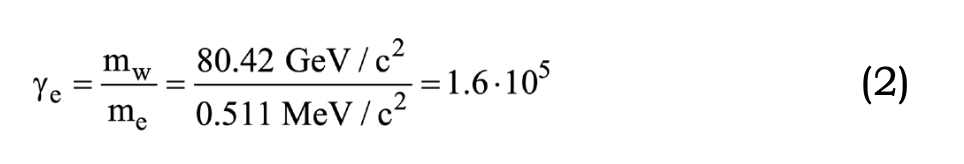
Consequently, for γ_e=1.6•10⁵ the corresponding γν₃, γν₂ and γν₁ Lorentz factor values for the three neutrinos are:

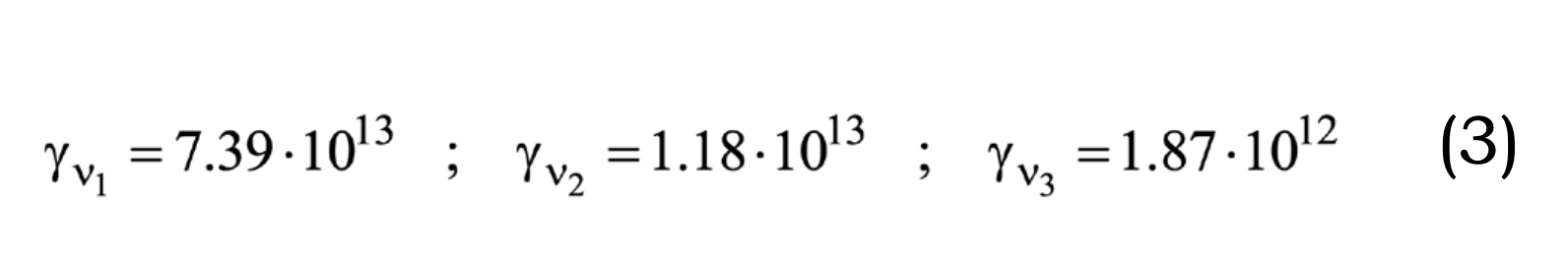
These very large γ_i values imply the onset of hadronization via formation of neutrons and protons. The corresponding gravitational masses, i.e. γ³_o,i m_o,i exceed the Planck mass by more than seven orders of magnitude.

This amazing result implies that the gravitational force between such relativistic neutrinos at a distance d can reach or even exceed the strong force value of ћc/d².

One may thus observe (Fig. 4) that such rotating positron (or electron) -neutrino rings, which correspond to W^± bosons, can act as neutrino catapults in that, upon decomposition, they generate extremely active neutrinos suitable for hadronization, i.e. for the formation of hadrons, such as neutrons and protons [10].

ACKNOWLEDGMENTS

This research has been co-financed by the Foundation for Education and European Culture (IPEP) and by the A.G. Leventis Foundation.

References

1. R.L. Workman et al. (Particle Data Group) (2022) The review of particle physics. Prog. Theor. Exp. Phys 2022:083C01
2. R. Serway, C. Moses, C. Moyer (2004) Modern Physics, Cengage Learning, Boston.
3. Takaaki Kajita, Nobel Lecture (2016): Discovery of Atmospheric Neutrino Oscillations. Rep. Prog. Phys. 69, 1607-1635 (2006).
4. L. Boltzmann (1964), Lectures on gas theory, Berkeley, CA, USA: U. of California Press.
5. “Catalysis in Chemistry and Physics: The Roles of Leptons, Special Relativity and Quantum Mechanics”, C.G. Vayenas, D.G. Tsousis, E.H. Martino, Springer Nature, Switzerland AG, (2024). ISBN978-3-031-68121-9.
6. D. Griffiths (2008) Introduction to Elementary Particles. 2nd ed. Wiley-VCH Verlag GmbH & Co. KgaA, Weinheim.
7. A.P. French (1968) Special relativity. W.W. Norton and Co., New York.
8. A. Einstein (1905) Zür Elektrodynamik bewegter Körper. Ann. der Physik., Bd. XVII, S. 17:891-921; English translation On the Electrodynamics of Moving Bodies (http://fourmilab.ch/etexts/einstein/specrel/www/) by G.B. Jeffery and W. Perrett (1923).
9. C.G. Vayenas, S. Souentie, A. Fokas. A Bohr-type model of a composite particle using gravity as the attractive force, Physica A, 405, 360-379 (2014).
10. C.G. Vayenas and D.G. Tsousis. The catalytic role of Electrons and Positrons in the synthesis of Chemicals and of Hadrons, Top. Catal. 66, 1280-1284 (2023).