Why black holes cannot exist?

1) INTRODUCTION:

When E. Beltrami introduced in 1892 the six stress functions Φij = Φji wearing his name and allowing to parametrize the Cauchy stress equations of elasticity theory in space, he surely did not know he was using the Einstein operator introduced by A. Einstein in 1915 for general relativity in space-time, both ignoring that it was self-adjoint in the framework of differential double duality and confusing therefore stress functions with the variation Ωij = Ωji of the metric ω. When I proved in 1995 [1, 6] that the Einstein equations could not be parametrized like the Maxwell equations, solving negatively a 1000 dollars challenge of J. Wheeler in 1970, contrary to the general belief of the GR community, I did not imagine that such a purely mathematical result could prove that the equations of the gravitational waves were not coherent with differential homological algebra and that black holes cannot exist because their existence contradicts the link existing between the Janet and Spencer sequences. Indeed, the last sequence is isomorphic to the tensor product of the Poincaré sequence by a Lie algebra of dimension 2 < 4 < 10 for the Kerr, Schwarzschild and Minkowski metrics with parameters (m, a), (m, 0) and (0, 0) [4].

When M. Janet introduced in 1920 the first finite length differential sequence as a footnote of a paper, he did not know about the possibility to use such a sequence in elasticity theory along the way introduced by the brothers E. and F. Cosserat in 1909. Taking the risk in 1970 to become a visiting student of D. C. Spencer (1912-2001) at Princeton University, I discovered that he was not knowing the mathematical foundations of general relativity studied by his close friend J. A. Wheeler (1911-2008). After 1995. being also a specialist of control theory, I decided to study the origin of GW and black holes by comparing the M, S and K metrics but also as a way to disagree with L. Andersson and collaborators met while lecturing at the Albert Einstein Institute (AEI) of Potsdam (October 23-27, 2017) [3].

In the Special Relativity paper of Einstein (1905), only a footnote provides a reference to the conformal group of space-time preserving the Minkowski metric ω up to a function factor but there is no proof that this conformal factor should be equal to 1. The conformal group of transformations of a manifold of dimension n has n translations, n(n − 1)/2 rotations, 1 dilatation and n highly non-linear elations introduced by E. Cartan in 1922. Using new mathematical tools and a clever paper of H. Poincaré, I have been able to prove the conformal origin of electromagnetism and gravitation in a coherent way with the dream of H. Weyl in 1918 [7]. When n = 4, the main idea is thus not to shrink the group from 10 down to 4 or 2 parameters by using the Schwarzschild or Kerr metrics instead of the Minkowski metric, but to enlarge the group from 10 to 11 or 15 parameters by using the Weyl or conformal group instead of the Poincaré group of space-time. These results bring the need to revisit the mathematical foundations of General Relativity and Gauge Theory but also question the origin and existence of gravitational waves and black holes.

2) MOTIVATING EXAMPLE:

Let us consider the second order system R₂ ⊂ J₂(E) written Qξ ≡ d₂₂ξ − b x²d₁ξ = η², Pξ ≡ d₁₂ξ − a d₁₁ξ = η¹ as an operator Dξ = η with coefficients in the ground differential field K = Q(x¹, x²) and P,Q ∈ D = K[d₁, d₂]. We may consider:

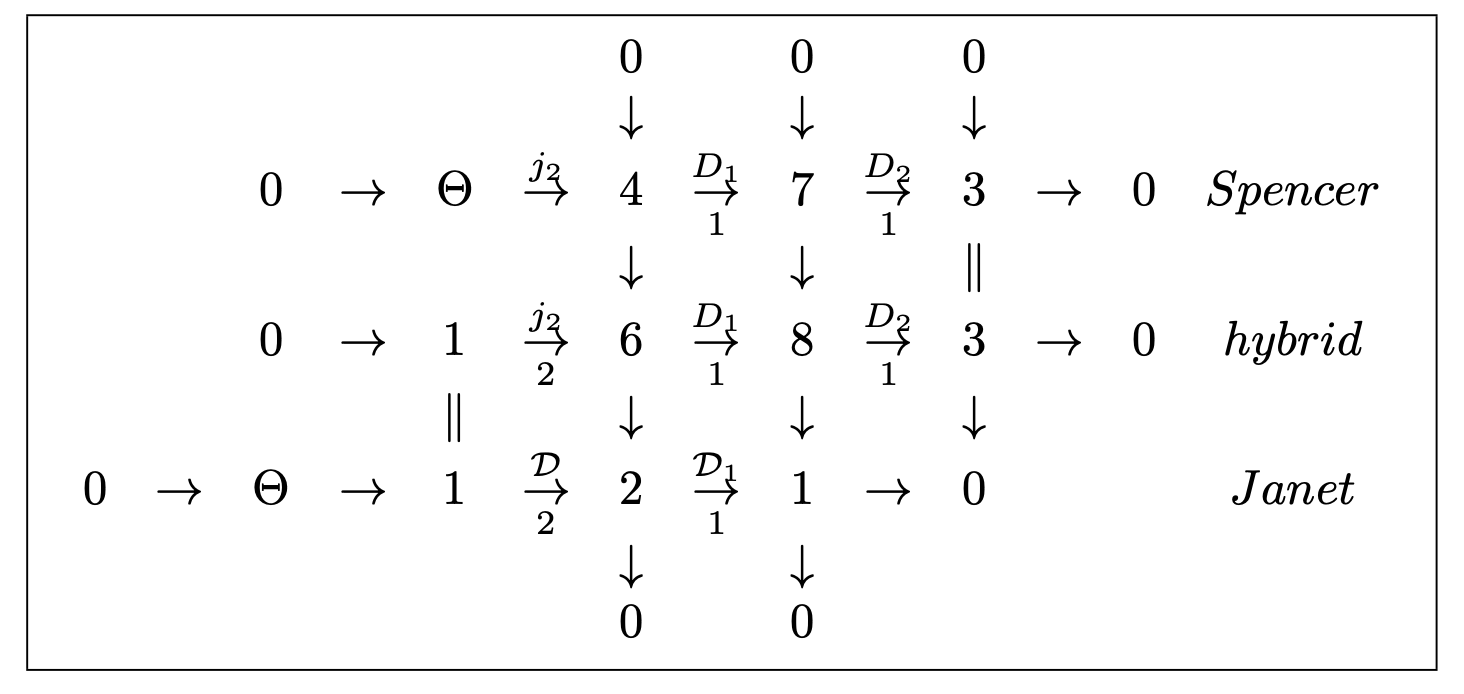
• a = 0, b = 0: Along with Janet, R₂ ⊂ J₂(E) is involutive with 4 parametric jets (z¹, …, z⁴) = (ξ, ξ₁, ξ₂, ξ₁₁) and one compatibility condition (CC) d₁η² −d₂η¹ = 0 defining a first order operator D1. Along with Spencer we may consider the first order involutive system R₃ ⊂J₁(R₂) defined by 7 equations through an operator D₁ with 3 CC through an operator D₂.

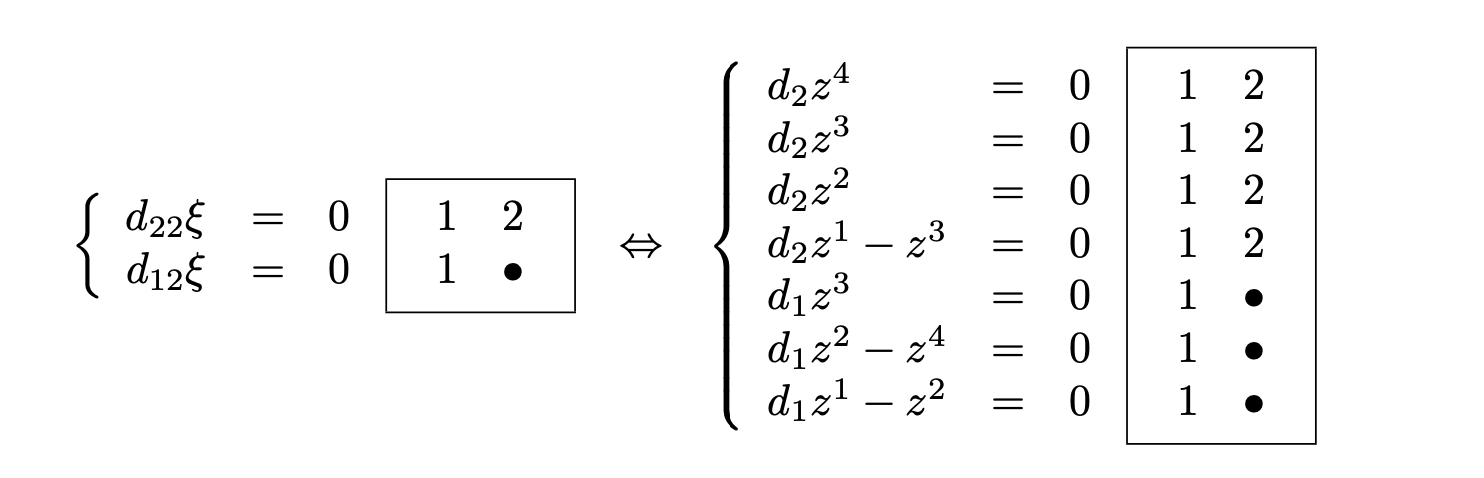
The Janet approach does not bring anything more or less that the Spencer approach as we have:

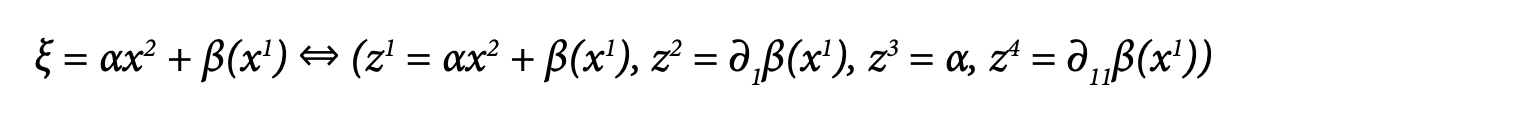
With j₂ = (1, d₁, d₂, d₁₁, d₁₂, d₂₂) ∈ D, the commutative Fundamental Diagram I becomes [1, 3, 6]:

Multiplying the only CC by the test function λ, we obtain the adjoint operator ad(D₁) : λ → (d₂λ = μ¹,−d₁λ = μ²) and similarly the adjoint operator ad(D) : μ → d₂₂μ² + d₁₂μ¹ = ν while the CC of ad(D₁) is d₁μ¹ + d₂μ² = 0 and the dual sequences are not exact at 2 and 7 [1, 4]:

• a = 1, b = 0 We have the second order CC Pη² − Qη¹ = [P,Q]ξ = 0 or D₁η = 0 in the duality:

We notice that ad(D) generates the CC of ad(D₁) and R₃ ⊂ J₃(E) is involutive with g₃ = 0 [8]:

• a = 1, b = 1: Differentiating once, we obtain the system R₃ ⊂ J₃(E) with symbol g₃ = 0 trivially involutive but the system is not FI. We have the strict inclusions R′₂ = R⁽²⁾₂ ⊂ R⁽¹⁾₂ = R₂ ⊂ J₂(E) with respective dimension 3 < 4 = 4 < 6 and obtain the new second order PD equation:

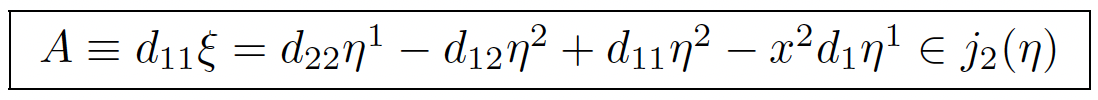
The hard step is to look for generating CC in the form of an operator D₁η = 0. There cannot exist any second order CC and we may start afresh with the new involutive system R′₂ = R⁽²⁾₂ :

Checking the two dots separately we have the two third order (!) CC:

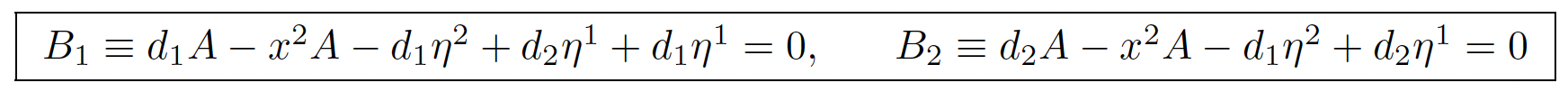
Using sections of jet bundles instead of derivatives, the Spencer operator D₁ becomes [3]:

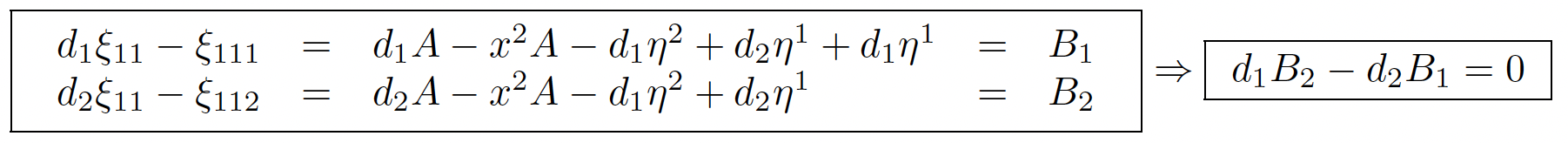
We have also the exact differential sequence which is not a Janet sequence:

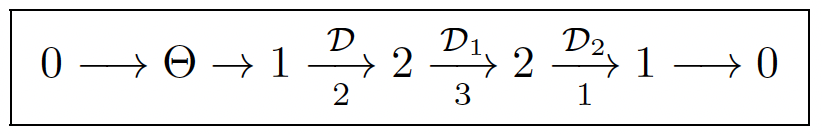
Using the basis {θτ (x) | 1 ≤ τ ≤ 3} = {1, x², x¹ + 1/6 (x²)³} for the vector space V of solutions over the field Q, the Spencer sequence of the Fundamental Diagram I is the tensor product by V of the Poincaré sequence ∧⁰T* ^d→ ∧¹T* ^d→ ∧²T*→ 0 for the exterior derivative when n = 2. Hence, depending on the parameters (a, b), we successively got first, second or third order CC.

3) FROM LIE GROUPS TO DIFFERENTIAL SEQUENCES:

Let G be a Lie group with coordinates (a^ρ) = (a¹, …, a^p) acting on a manifold X with a local action map y = f(x, a). According to the second fundamental theorem of Lie, if {θτ | 1 ≤ τ ≤ p = dim(G)} are the infinitesimal generators of the effective action of a lie group G on X, then [θ_ρ, θ_σ] = c^τ_ρσθ_τ where the c = (c^τ_ρσ = −c^τ_σρ) are the structure constants of a Lie algebra of vector fields which can be identified with G = T_e(G) the tangent space to G at the identity e ∈ G by using the action.

More generally, if X is a manifold and G is a lie group (not acting necessarily on X), let us consider gauging maps a : X → G : (x) → (a(x)). If x + dx is a point of X close to x, then T(a) will provide a point a + da = a + ^∂a/_∂x dx close to a on G. We may bring a back to e on G by acting on a with a⁻¹, on the left, getting therefore a 1-form a⁻¹da = A ∈ T* ⊗ G and the curvature 2-form F = (∂_iA^τ_j (x) − ∂_jA^τ_i (x) − c^τ_ρσ A^ρ_i (x)A^σ_j (x) = F^τ_ij(x)) ∈ ∧²T* in the nonlinear gauge sequence:

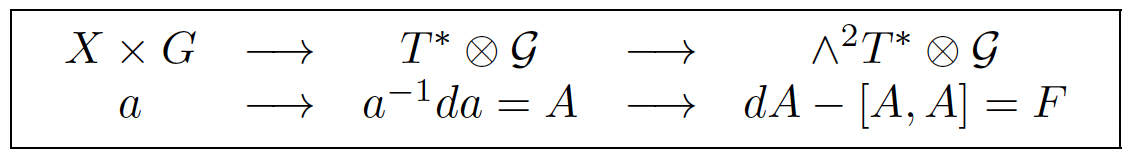
In 1956, at the birth of gauge theory (GT), the above notations were coming from the EM potential A and EM field dA = F of relativistic Maxwell theory and G = U(1) (unit circle in the complex plane) was the only possibility to get a 1-form A and a 2-form F with c = 0 [1]

Choosing now a “close” to e, that is a(x) = e + tλ(x) + … and linearizing as usual, we obtain the linear operator d : ∧⁰T* ⊗ G → ∧¹T* ⊗ G : (λ^τ (x)) → (∂_iλ^τ (x)) and the linear gauge sequence:

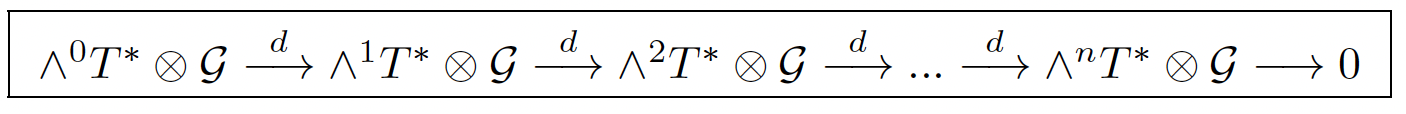
which is the tensor product by G of the Poincaré sequence for the exterior derivative.

In a different setting, If μ = (μ₁, …, μ_n) is a multi-index of length | μ |= μ₁ + … + μ_n and μ + 1_i = (μ₁, .., μ_i−1, μ_i + 1, μ_i+1, …, μ_n), we may introduce a system R_q ⊂ J_q(T) with sections defined by ξ^k_μ (x) = λ^τ (x)∂_μθ^k_τ (x) for an arbitrary section λ ∈ ∧⁰T* ⊗G and the trivially involutive operator j_q : T → J_q(T) : θ → (∂_μθ, 0 ≤| μ |≤ q) of order q. We finally obtain the Spencer operator through the chain rule for derivatives:

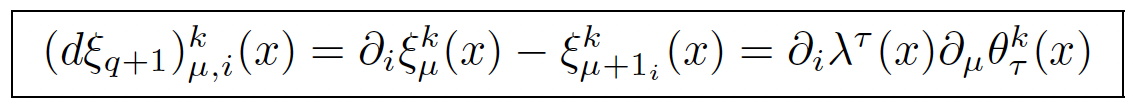
When q is large enough to have g_q = 0 and thus an isomorphism R_q+1 ≃ R_q ≃ ∧⁰T* ⊗ G and the following linear Spencer sequence in which the operators D_r are induced by d as above:

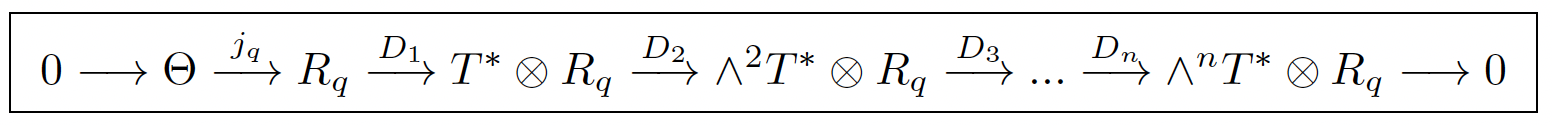
is isomorphic to the linear gauge sequence but with a completely different meaning because G is now acting on X and Θ ⊂ T is such that [Θ, Θ] ⊂ Θ. The system R_q ⊂ J_q(T) is a Lie algebroid if [R_q, R_q] ⊂ R_q and [R^(s)_q+r , R^(s)_q+r ] ⊂ R^(s)_q+r , ∀r, s ≥ 0 thanks to the following definitions and formulas that can be extended to arbitrary Lie pseudogroups:

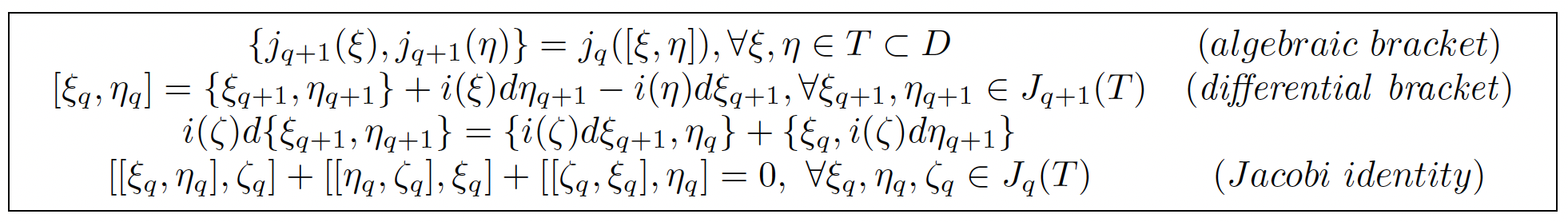
in which i(ξ)dη_q+1 means the contraction of a 1-form in T* ⊗ R_q by a vector field ξ ∈ T.

4) APPLICATIONS:

This situation is similar to that of the Killing system R₁ ⊂ J₁(T) defined by the first order Killing operator D : T → S₂T* : ξ → L(ξ)ω = Ω through the Lie derivative of a nondegenerate metric ω. Such an operator is FI iff the metric has a constant Riemannian curvature, for example in the case of the M metric, but far from being FI in the cases of the S or K metrics.

The Prolongation/Projection (PP) procedure may provide convenient integers (r, s) leading to a FI system

and to the strict inclusions R⁽³⁾₁ ⊂ R⁽²⁾₁ ⊂ R⁽¹⁾₁ = R₁ for the Killing system and its prolongations/projections that must be done. Using the Lie algebra G with dimension 10 for M, 4 for S and 2 for S instead of V, the previous results show that the Spencer sequence is isomorphic to the tensor product of the Poincaré sequence by this Lie algebra [4, 5, 6]:

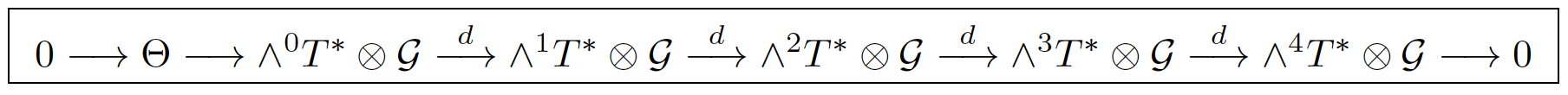
In Boyer-Lindquist coordinates (t, r, θ, ϕ) = (x⁰, x¹, x², x³), we may write the Schwarzschild diagonal metric as ω = A(r)dt² − (1/A(r))dr² − r²dθ² − r²sin²(θ)dϕ² and ξ = ξⁱd_i ∈ T ⊂ D. With speed of light c = 1 and A = 1− ^m/r ⇒ A′ = ∂_rA = ^m/_r2 where m is a constant, the Killing equations and their first prolongations with Christoffel symbols γ become:

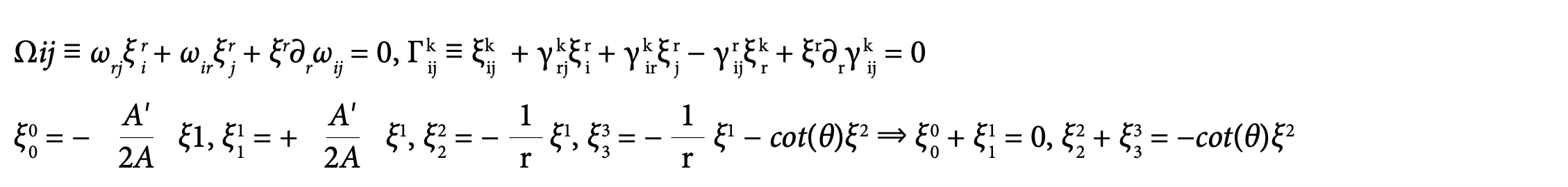
Since the 6 non-zero components (ρ_kl,ij) ∈ ∧²T* ⊗T* ⊗T* of the Riemann tensor are known from computer agebra, we may add the 20 − 10 = 10 linearized first order equations:

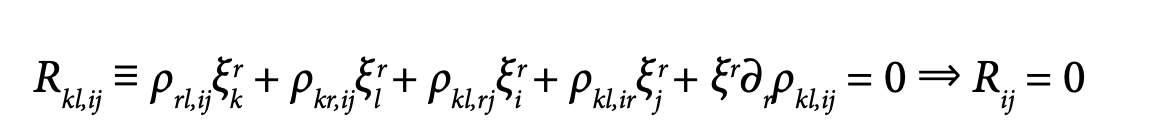
However, as we are dealing with sections, ξ1 = 0 implies ξ⁰₀ = 0, ξ^1/₁ = 0, ξ^2/₂ = 0 but NOT (care) ξ^1/₀ = 0, this condition being only brought by one additional prolongation. We have the inclusions R⁽³⁾₁ ⊂ R⁽²⁾₁ ⊂ R⁽¹⁾₁ = R1 ⊂ J₁(T) of Lie algebroids with dimensions 4 < 5 < 10 = 10 < 20.

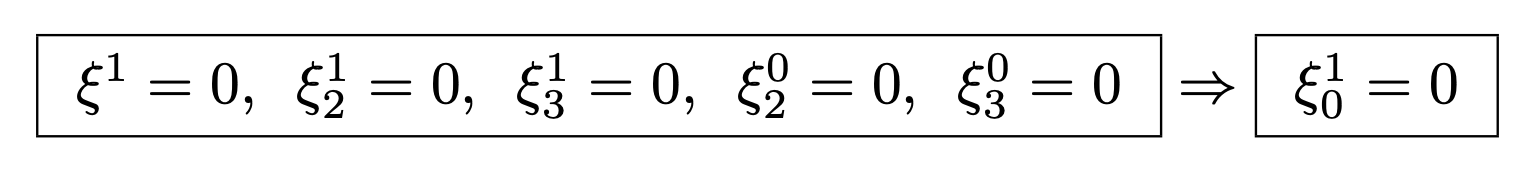
The group of invariance (1 time translation + 3 space rotations) does not depend on m any longer and the Spencer sequence, tensor product of the Poincaré sequence by its Lie algebra, becomes:

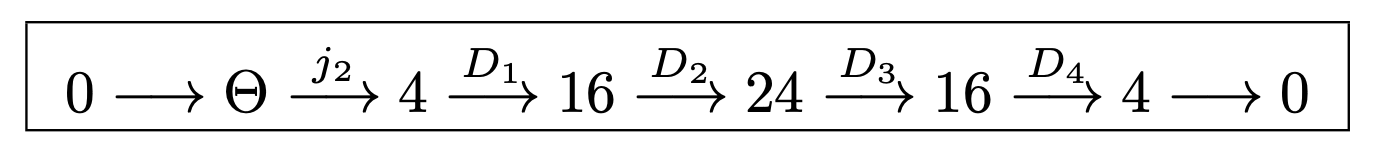
The Killing operator for the S metric has 15 second order CC because of the long exact sequence:

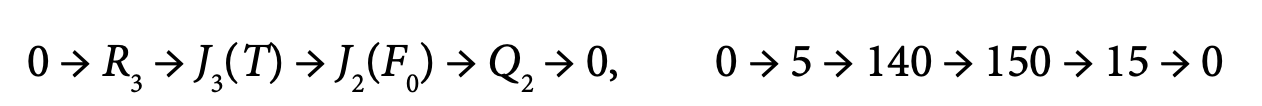
and 3 third order CC because of the Spencer operator (Compare to the previous page !):

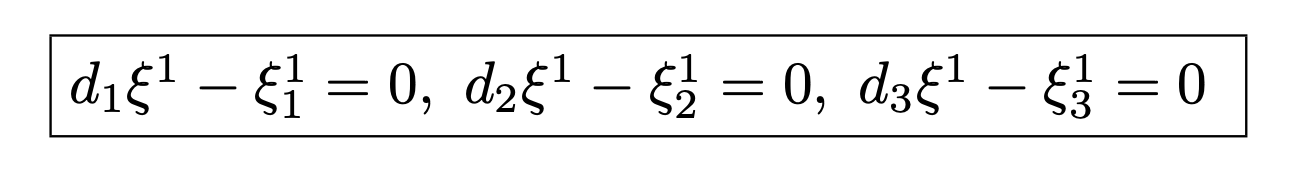
For the Kerr metric, we get 2 < 4 < 10 = 10 < 20, 14 second order CC and 6 third order CC:

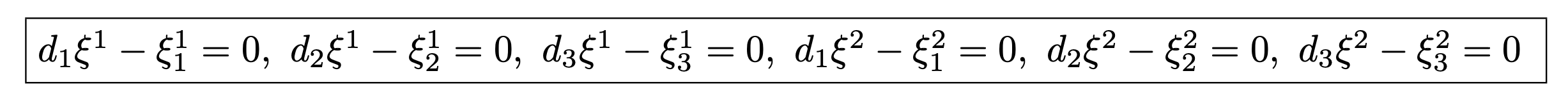
THE IMPORTANT OBJECT IS NOT THE METRIC BUT ITS GROUP OF INVARIANCE