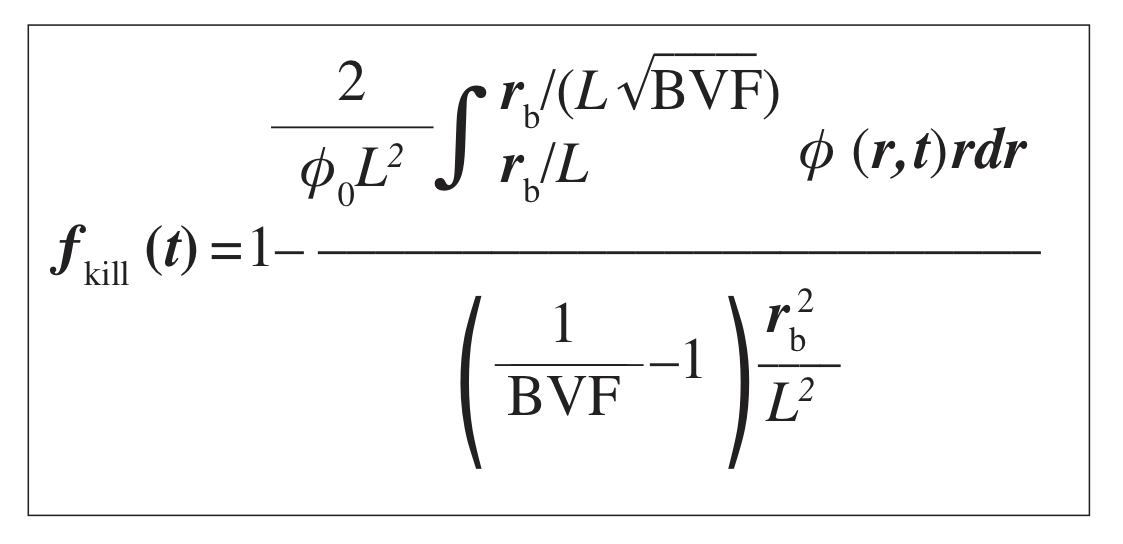Zhihui Wang and Vittorio Cristini provide evidence that could improve the success of treatment plans and make predicting cancer treatment outcome easier
Current processes for creating cancer treatment plans are primarily based on empirical data from clinical trials, consensus expert panel guidelines, and limited laboratory-based testing. Physicians still face major challenges in successful prediction of the effectiveness of any particular treatment plan for any given patient, prior to actual treatment. Physical oncology is an integrated approach that focuses on developing mechanistic models to provide predictions of treatment outcomes based on biophysical and biological parameters that can be gained from individual tumours in specific patients. This approach can not only help improve treatment outcomes, but it could also benefit many cancer patients if incorporated into the creation of treatment plans.
Here, we provide evidence for improving cancer treatment plan efficacy, through the inclusion of mathematical modelling techniques, based on our capability to consider the multiple scales of the human body, (i.e., cellular, tissue, and organ) when predicting patient-specific treatment outcomes. We developed a mathematical model that accounts for diffusion on a tissue-scale, in addition to cellular and genetic influences, in order to bridge a gap in understanding and predicting tumour response to anticancer therapies.1 We extended a time-dependent model by incorporating spatial dependence to describe perfusion and diffusion heterogeneities.2
By integrating the viable tumour volume fraction (BVF), at each time point over the cylindrical tissue domain surrounding a blood vessel and affected by the drug diffusion, we calculate ƒkill as the ratio of the killed tumour volume to the total initial tumour volume:
As a function of parameters: rb (blood vessel radius), BVF, and L=√D/(φ0λu) (the effective diffusion penetration length of the drug).
We performed a set of simulations with the time and space dependent model in a cylindrically symmetric domain surrounding a blood vessel. Model parameter values were set as follows: L = 155.06 μm and rb = 15.83 μm – based on experimentally measured values in resected patient colorectal metastasis to liver tumours – giving rb/L = 0.102; we also set BVF = 10-2 as the reference value for the simulations, as measured BVF values ranged approximately from 10-3 to 10-1.3
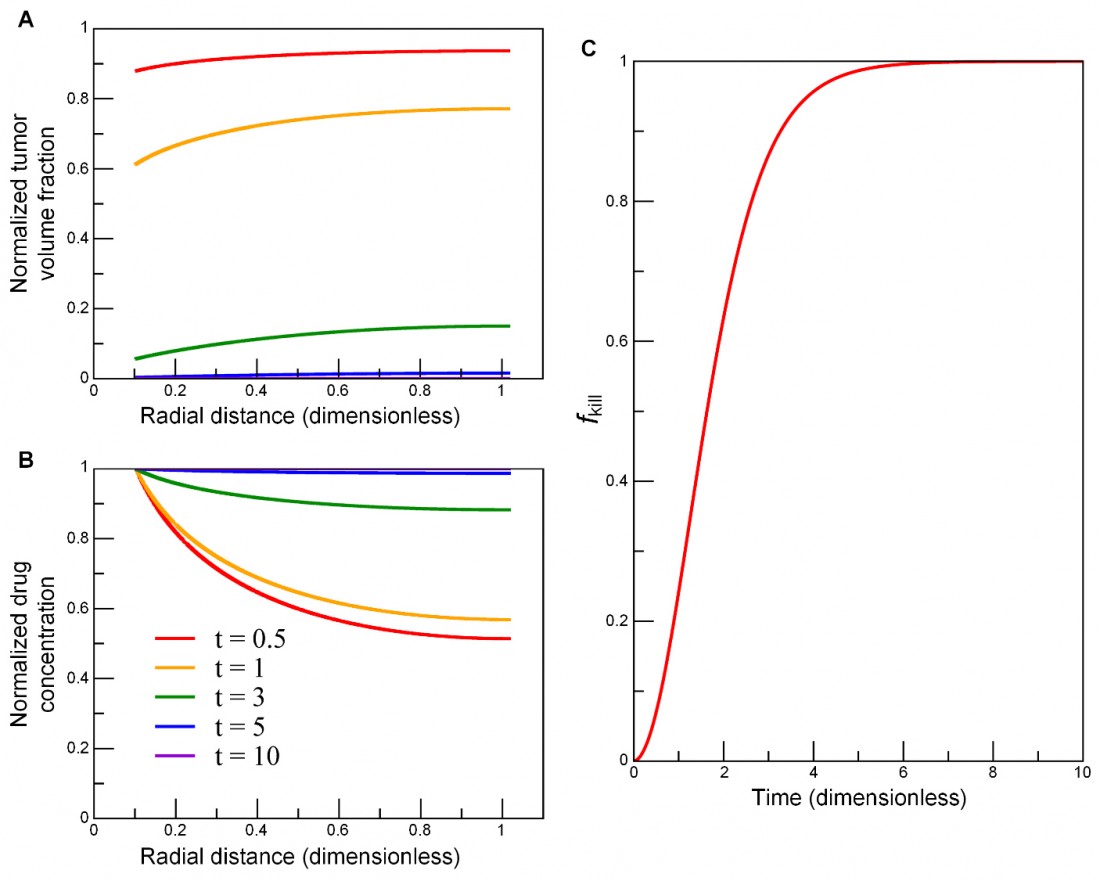
To examine the impact of each parameter on ƒkill, we simulated nine parameter-variation combinations, using three rb/L values, i.e., 0.05, 0.1, 0.5, paired with three BVF values, i.e., 0.005, 0.01, 0.05. Figure 1 shows the numerical results of the model. In the presence of a boundary condition σ0 at the vessel wall (r = rb), successive cell layers next to the blood vessel die out (Fig. 1A) due to cell-death induced enhancement of drug penetration (Fig. 1B), in turn leading to accelerated cell kill (Fig. 1C). As cell kill occurs, tumour volume fraction φ decreases, leading to an increase in local drug concentration σ (because dead cells no longer uptake drugs), and thus accelerating cell kill in the locations further away from the vessel and deeper into the tumour.
Fig. 1: Numerical simulations of the model in a cylindrically symmetric domain. As cell kill ensues over several cell cycles, (A) successive cell layers next to the blood vessel (r = rb) die out, i.e., tumour volume fraction φ decreases (top to bottom: t = 0.5, 1, 3, 5, 10); (B), local drug concentration σ increases due to an enhancement of drug penetration (bottom to top: t = 0.5, 1, 3, 5, 10); and (C) cell kill accelerates further from the vessel and deep into the tumour. Input parameters: rb/L = 0.102 and BVF = 0.01. The duration of the entire simulation was 10 (λkλuφ0σ0)-1/2, where time unit is a characteristic cell apoptosis time. Drug concentration and tumour volume fraction were normalised by their initial values, and radial distance by the diffusion penetration distance L. The fraction of tumour kill ƒkill is calculated from Eq. 1.4
As evidenced in this modelling study, we have shown that tissue-scale factors significantly affect a drug’s ability to kill cancer. Focusing on this scale allowed us to observe the tumour microenvironment’s impact on drug delivery, which revealed the presence of diffusion barriers, which prevent adequate concentrations of drug from reaching the tumour cells. Not only did we find that tissue-scale barriers impact drug delivery and effectiveness, but that diffusion barriers may be a main cause for drug resistance in many tumours. If the sources of drug resistance can be determined, it is our hope that researchers and physicians can create strategies to overcome them, thus drastically improving treatment outcomes.
References
1 Wang et al., PLoS Comput Biol 2016, PMC4902302
2 Pascal et al., ACS Nano 2013, PMC3891887
3 Pascal et al., PNAS 2013, PMC3761643
4 Reproduced from (Wang et al., PLoS Comput Biol 2016, PMC4902302).
Additional resources
http://www.internationalinnovation.com/taking-cancer-out-of-the-equation/
http://www.jci.org/articles/view/73455
http://www.pnas.org/content/110/35/14266.long
http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1004969
Zhihui Wang and Vittorio Cristini
Center for Precision Biomedicine, Brown Foundation Institute of Molecular Medicine
University of Texas Health Science Center at Houston (UTHealth) McGovern Medical School
Tel: +1 713 486 2315
Please note: this is a commercial profile