Extreme weather events may cause severe damage to our society. Examples include hurricane Sandy in 2012 (the second-costliest hurricane in United States history), European windstorms Lothar and Martin in 1999, and, more recently, the exceptional sequence of floods in southern England in the winter of 2014. Insurance companies need to reserve sufficient capital to cover claims following an extreme weather event. Estimates of expected losses due to catastrophic events crucially depend on the tail width of the probability distribution describing the likelihood of extremes. Hence, understanding the typical tail behaviour of time series generated by climate models is a pressing challenge for the insurance industry and forecasting agencies.
Our research
The Johann Bernoulli Institute for Mathematics and Computer Science (JBI), based at the University of Groningen, actively participates in current mathematical research on extreme events. The mission of the JBI is the cross-fertilization by modelling of the disciplines mathematics and computer science both with other sciences and with the outside world.
Prof Henk Broer is an internationally renowned expert in Nonlinear Dynamical Systems. Dr Alef Sterk has worked on the mathematical analysis of climate models. We collaborate with Dr Renato Vitolo, Dr Mark Holland (Exeter), and Dr Pau Rabassa (London) who provide us with expertise on climate modelling and ergodic theory. Prof Carles Simo (University of Barcelona) complements our research with state of the art numerical methods for deterministic systems and background mechanisms. We are embedded in a larger, international network of scientists working on extreme events and its applications to climate science.
Mathematical climate modelling
Mathematical modelling offers a fruitful approach towards an understanding of meteo-climatic extremes. Models for the atmospheric and oceanic circulation are typically derived from first principles, such as Newton’s laws, conservation of energy, global balances, etc. This approach leads to deterministic evolution laws in which the present state of the system completely determines its future.
However, since the seminal work of the mathematician and meteorologist E.N. Lorenz in the 1960s it is well known that even deterministic systems can be very unpredictable: small perturbations in the initial state may lead to large differences in later states, see Figure 1. This phenomenon, which is colloquially known as the butterfly effect, hampers long-term weather forecasts and triggered the development of mathematical research on nonlinear dynamics and chaos theory.
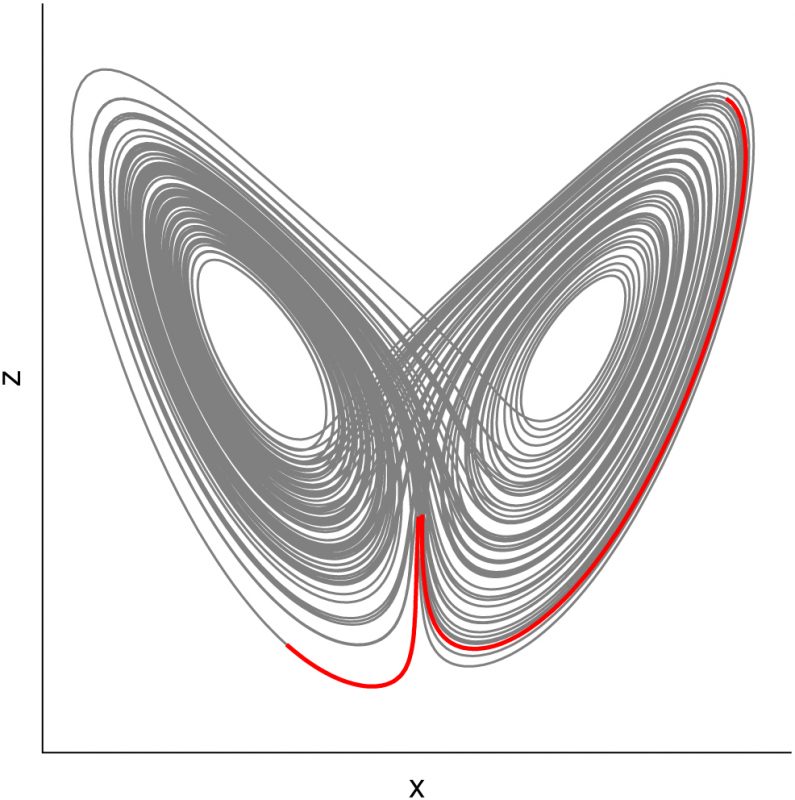
Our achievements
Our research is strongly interdisciplinary. Our expertise includes nonlinear dynamical systems, extreme value statistics, and climate modelling. This unique combination enables us to tackle both theoretical and applied problems on extreme weather events.
Storm clustering
Intense windstorms are a major cause of damage in Europe. Such meteorological extremes may occur in groups (clusters), such as the December 1999 windstorms Anatol, Lothar, and Martin, which produced total damage exceeding $15 B. Such storm clustering is particularly threatening for insurance companies.
We discovered that clustering tends to be stronger for the more intense windstorms over Europe. We analysed how this is related to the time-varying effect of the large-scale atmospheric flow. Specifically, certain features of the atmospheric dynamics, the so-called teleconnection patterns (such as the North Atlantic Oscillation) are found to induce temporal modulation in the windstorm arrival rate. This may lead to the occasional accumulation of several extremes within relatively short time spans.
Analogous explanations have been provided for the clustering of other meteo-climatic extremes, such as intense tropical cyclones (hurricanes, typhoons) and floods, providing enhanced statistical models for the occurrence of such phenomena.
For more details, see:
- R. Vitolo, D.B. Stephenson, I.M. Cook, and K. Mitchell-Wallace. Serial clustering of intense European storms. Meteorologische Zeitschrift 18(4), pp. 411-424, 2009.
- P.J. Mumby, R. Vitolo, and D.B. Stephenson. Temporal clustering of tropical cyclones and its ecosystem impacts. Proceedings of the National Academy of Sciences, 10(43), pp. 17626-17630, 2011.
- G. Villarini, J.A. Smith, R. Vitolo, and D.B. Stephenson. On the temporal clustering of US floods and its relationship to climate teleconnection patterns. International Journal of Climatology, 33(3), pp. 629-640, 2013.
Estimating the tail index
Classical extreme value theory studies the distribution of large values in time series of independent random variables. Since the early 2000s the theory has been extended to deterministic systems, such as climate models. In this setting the so-called Generalised Extreme Value (GEV) distributions can be used to compute the probability of occurrence of future large values of a quantity, such as wind speed or sea surface level, given a sample of past measurements.
To that purpose one must estimate a couple of unknown parameters of the distribution. Of particular importance is the so-called tail index because it determines the tail width of the distribution, and therefore the frequency and intensity of extreme events. Accurate estimates of the tail index are useful for forecasting agencies like the UK MetOffice and the Royal Netherlands Meteorological Institute or reinsurance brokers like Willis Re.
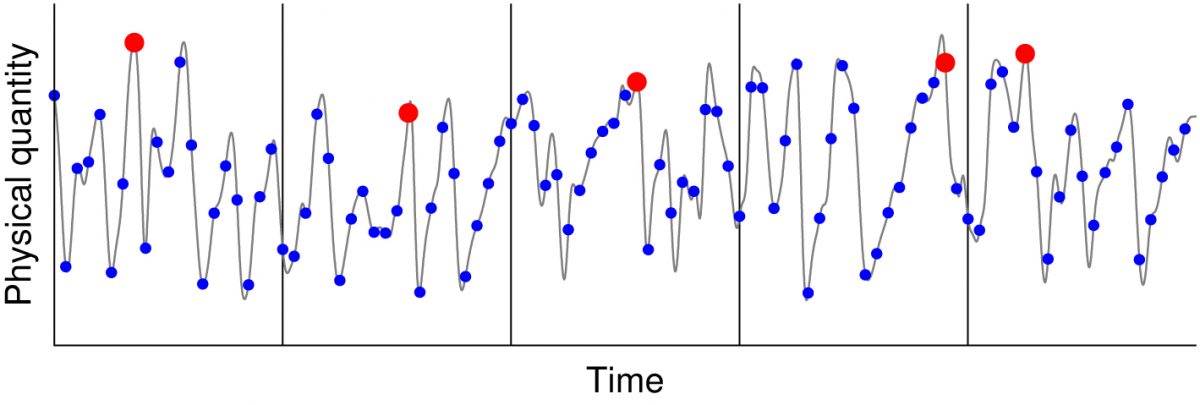
Estimates for the tail index are often obtained by the so-called block maximum method, see Figure 2. In this method one divides a time series, either obtained from data or numerical simulations, in sufficiently long blocks. Under the assumption that the block maxima form a random sample drawn from a GEV distribution the parameters can be estimated using standard statistical methods. Recently, we discovered that the tail index is related to the geometry of the evolutions of the underlying dynamical system, such as the fractal dimension of the attractor. This discovery also explains why sometimes prohibitively long time series are needed to obtain accurate estimates.
For more details, see:
- M.P. Holland, R. Vitolo, P. Rabassa, A.E. Sterk, and H.W. Broer. Extreme value laws in dynamical systems under physical observables. Physica D: Nonlinear Phenomena 241(5), pp. 497-513, 2012.
Predictability of extremes
We have studied the finite-time predictability of extreme values, such as convection, energy, and wind speeds, in geophysical models. To that purpose we computed the exponential growth rates (Lyapunov exponents) of nearby trajectories over a finite time interval. In general these growth rates strongly depend on the initial condition, see Figure 3.
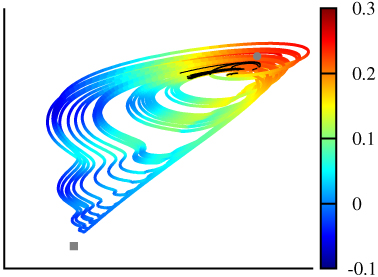
We studied whether initial conditions leading to extremes typically have a larger or smaller error growth rate. We addressed this question using simplified models for the atmospheric circulation. Our results clearly suggest that the predictability of extreme events strongly depends on the type of event. For example, the predictability of extreme wind speeds strongly depends on the geographical location of interest: extreme wind speeds are typically better predictable in valleys than on mountain tops. This conclusion warrants a further in-depth study on how extreme events depend on landscape characteristics.
For more details, see:
- A.E. Sterk, M.P. Holland, P. Rabassa, H.W. Broer, and R. Vitolo. Predictability of extreme values in geophysical models. Nonlinear Processes in Geophysics 19(5), pp. 529-539, 2012.
Funding our research
Our past research projects have been funded by the Netherlands Organisation for Scientific Research (NWO) and the Engineering and Physical Sciences Research Council (EPSRC) under the auspices of Complexity-NET. We are interested in new funding opportunities in order to expand our research activities. New projects will lead to novel mathematical techniques for studying extremes in climate models and data. In addition, funding provides the means to educate junior scientists. There are not many mathematicians trained in the application of extreme value theory to climate models and there is a need to increase this pool.
Contact details
Prof Dr Henk W. Broer
Professor of Dynamical Systems
Johann Bernoulli Institute for Mathematics and Computer Science
Telephone: +31 50 363 3959
Dr Alef E. Sterk
Assistant Professor
Johann Bernoulli Institute for Mathematics and Computer Science
Dr Renato Vitolo
Honorary Research Fellow
University of Exeter
Dr Mark P. Holland
Senior Lecturer in Mathematics
University of Exeter
Dr Pau Rabassa Sans
Postdoctoral Researcher
Queen Mary, University of London








